��Ŀ����
����Ŀ����ͼ��ʾ����ֱ������ABCD����AD//BC����A��90����AB��12��BC��21��AD=16������P�ӵ�B������������BC�ķ�����ÿ��2����λ�����ٶ��˶�������Qͬʱ�ӵ�A���������߶�AD����ÿ��1����λ�����ٶ����D�˶���������һ�����㵽��˵�ʱ��һ������Ҳ��ֹ֮ͣ�˶������˶���ʱ��Ϊt��������
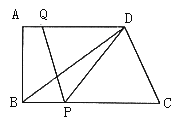
��1������DPQ�����ΪS���ú���t�Ĵ���ʽ��ʾS��
��2����tΪ��ֵʱ���ı���PCDQ��ƽ���ı��Σ�
���𰸡���1��S=96��6t����2��t=5��
��������
�����������1�����Ƚ�QD�ij����ú�t�Ĵ���ʽ����ʾ��Ȼ��ó������ε������t֮��Ĺ�ϵ����2������ƽ���ı��ε��ж������ó�OD=PC���г�����t��һԪһ�η��������t��ֵ��
�����������1����������ã�AQ=t����QD=16-t
��S=![]() ��16��t����12=96��6t
��16��t����12=96��6t
��2����AD��BC
����QD=PCʱ���ı���PCDQ��ƽ���ı���
��BP=2t
��PC=21-2t
��16-t=21-2t
��t=5
�𣺵�tΪ5��ʱ���ı���PCDQ��ƽ���ı���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

