题目内容
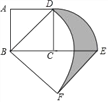
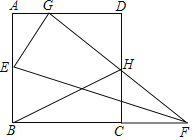
【题目】如图,已知正方形ABCD,点E在AB上,点F在BC的延长线上,将正方形ABCD沿直线EF翻折,使点B刚好落在AD边上的点G处,连接GF交CD于点H,连接BH,若AG=4,DH=6,则BH=_____.
【答案】6![]()
【解析】
通过证明△AEG∽△DGH,可得![]() =
=![]() ,可设AE=2a,GD=3a,可求GE的长,由AB=AD,列出方程可求a的值,由勾股定理可求BH的长.
,可设AE=2a,GD=3a,可求GE的长,由AB=AD,列出方程可求a的值,由勾股定理可求BH的长.
解:∵将正方形ABCD沿直线EF翻折,使点B刚好落在AD边上的点G处,
∴AB=AD=BC=CD,EG=BE,∠ABC=∠EGH=90°
∵∠AGE+∠DGH=90°,∠AGE+∠AEG=90°
∴∠AEG=∠DGH,且∠A=∠D=90°
∴△AEG∽△DGH
∴![]() =
=![]()
∴设AE=2a,GD=3a,
∴GE=![]() =
=![]()
∵AB=AD
∴2a+![]() =4+3a
=4+3a
∴a=![]()
∴AB=AD=BC=CD=12,
∴CH=CD﹣DH=12﹣6=6
∴BH=![]() =6
=6![]()
故答案为:6![]() .
.

练习册系列答案
相关题目