题目内容
【题目】已知二次函数![]() .
.
(1)证明:不论![]() 取何值,该函数图像与
取何值,该函数图像与![]() 轴总有公共点;
轴总有公共点;
(2)若该函数的图像与![]() 轴交于点(0,3),求出顶点坐标并画出该函数图像;
轴交于点(0,3),求出顶点坐标并画出该函数图像;
(3)在(2)的条件下,观察图像,解答下列问题:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有两个不相等的实数根,则
有两个不相等的实数根,则![]() 的取值范围是 ;
的取值范围是 ;
③若一元二次方程![]() 在
在![]() 的范围内有实数根,则
的范围内有实数根,则![]() 的取
的取
值范围是 .
【答案】(1)证明见解析;(2)顶点(1,4);作图略(3)①0<x<2;②k<4;③-5<t≤4
【解析】试题分析:(1)令y=0得到关于x的方程,找出相应的a,b及c的值,表示出![]() ,整理配方后,根据完全平方式大于等于0,判断出
,整理配方后,根据完全平方式大于等于0,判断出![]() 大于等于0,可得出抛物线与x轴总有交点,得证;
大于等于0,可得出抛物线与x轴总有交点,得证;
(2)由抛物线与y轴交于(0,3),将x=0,y=3代入抛物线解析式,求出m的值,进而确定出抛物线解析式,配方后找出顶点坐标,根据确定出的解析式列出相应的表格,由表格得出7个点的坐标,在平面直角坐标系中描出7个点,然后用平滑的曲线作出抛物线的图象,如图所示;
(3)由图象和解析式即可可求得.
试题解析:(1) ![]()
∴不论m取何值,该函数图象与x轴总有公共点,
(2)∵该函数的图象与y轴交于点(0,3),
∴把x=0,y=3代入解析式得:m=3,
![]()
∴顶点坐标为(1,4);
列表如下:
x | 2 | 1 | 0 | 1 | 2 | 3 | 4 |
y | 5 | 0 | 3 | 4 | 3 | 0 | 5 |
描点;
画图如下:
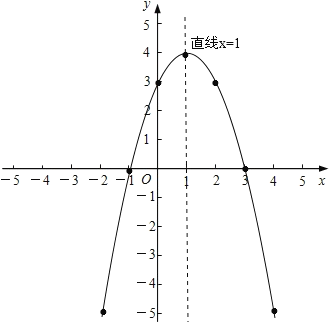
(3)根据图象可知:①不等式![]() 的解集是:0<x<2,
的解集是:0<x<2,
②由抛物线的解析式![]() 可知若一元二次方程
可知若一元二次方程![]() 有两个不相等的实数根,则k的取值范围是:k<4,
有两个不相等的实数根,则k的取值范围是:k<4,
③若一元二次方程![]() 在1<x<4的范围内有实数根,t的取值就是函数
在1<x<4的范围内有实数根,t的取值就是函数![]() 在1<x<4的范围内的函数值,由图象可知在1<x<4的范围内
在1<x<4的范围内的函数值,由图象可知在1<x<4的范围内![]() ,故
,故![]()
故答案为0<x<2,k<4, ![]()

【题目】某商店销售一种商品,通过记录,发现该商品从开始销售至销售的第x天结束时(x为整数)的总销量y(件)满足二次函数关系,销量情况记录如下表:
x | 0 | 1 | 2 | 3 |
y | 0 | 58 | 112 | 162 |
(1)求y与x之间的函数关系式(不需要写自变量的取值范围);
(2)求:销售到第几天结束时,该商品全部售完?
(3)若第m天的销量为22件,求m的值.
【题目】“赏中华诗词,寻文化基因,品生活之美”某校举办了首届“中国诗词比赛”,全校师生同时默写50首古诗,每正确默写出一首古诗得2分,结果有600名学生进入决赛,从进入决赛的600名学生中随机抽取40名学生进行成绩分析,根据比赛成绩绘制出部分频数分布表和部分频数分布直方图如下列图表
组别 | 成绩x(分) | 频数(人数) |
第1组 | 60≤x<68 | 4 |
第2组 | 68≤x<76 | 8 |
第3组 | 76≤x<84 | 12 |
第4组 | 84≤x<92 | a |
第5组 | 92≤x<100 | 10 |
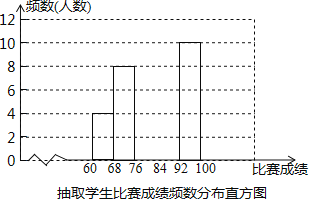
第3组12名学生的比赛成绩为:76、76、78、78、78、78、78、78、80、80、80、82请结合以上数据信息完成下列各题:
(1)填空:a= 所抽取的40名学生比赛成绩的中位数是
(2)请将频数分布直方图补充完整
(3)若比赛成绩不低于84分的为优秀,估计进入决赛的学生中有多少名学生的比赛成绩为优秀?