题目内容
如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(1)3;(2)B(-1,0).
解析试题分析:(1)由二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),利用待定系数法将点A的坐标代入函数解析式即可求得m的值;
(2)根据(1)求得二次函数的解析式,然后将y=0代入函数解析式,即可求得点B的坐标.
试题解析:(1)∵二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),
∴-9+2×3+m=0,
解得:m=3;
(2)∵二次函数的解析式为:y=-x2+2x+3,
∴当y=0时,-x2+2x+3=0,
解得:x=3或x=-1,
∴B(-1,0).
考点: 二次函数综合题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 与
与 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
 =7.14,
=7.14, =7.21,
=7.21, =7.28,
=7.28,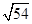 =7.35)
=7.35)
 (5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
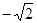 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.
 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
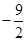 );Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为(
);Rt△ABC的直角边BC在x轴上,直角顶点C的坐标为( ,0),且BC=5,AC=3(如图1).
,0),且BC=5,AC=3(如图1).
 的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为(
的图象与x轴交于A、B两点, A点在原点的左侧,B点的坐标为( ,
, ),与y轴交于C(
),与y轴交于C( )点,点P是直线BC下方的抛物线上一动点.
)点,点P是直线BC下方的抛物线上一动点.
 中,抛物线
中,抛物线 过点
过点 ,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为
,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为 ,连接CA,CB,CD.
,连接CA,CB,CD.
 ;
; 是第一象限内抛物线上的一个动点,连接DP交BC于点E.
是第一象限内抛物线上的一个动点,连接DP交BC于点E.