题目内容
已知:如图,二次函数图象的顶点坐标为C(1,-2),直线y=kx+m的图象与该二次函数的图象交于A、B两点,其中A点坐标为(3,0),B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这个二次函数的图象交于点E.(1)求这个二次函数的解析式;
(2)设点P的横坐标为x,求线段PE的长(用含x 的代数式表示);
(3)点D为直线AB与这个二次函数图象对称轴的交点,若以点P、E、D为顶点的三角形与△AOB相似,请求出P点的坐标.

【答案】分析:(1)首先设二次函数的解析式为y=a(x-1)2-2,由A点坐标为(3,0),则可将A点的坐标代入函数解析式,利用待定系数法即可求得这个二次函数的解析式;
(2)首先利用待定系数法求得直线AB的解析式,然后由P在直线上,将x代入直线方程,即可求得P的纵坐标,又由E在抛物线上,则可求得E的纵坐标,它们的差即为PE的长;
(3)分别从当∠EDP=90°时,△AOB∽△EDP与当∠DEP=90°时,△AOB∽△DEP两种情况去分析,注意利用相似三角形的对应边成比例等性质,即可求得答案,注意不要漏解.
解答: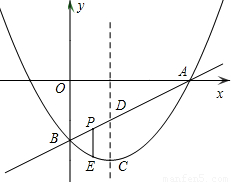 解:(1)设二次函数的解析式为y=a(x-1)2-2,
解:(1)设二次函数的解析式为y=a(x-1)2-2,
∵A(3,0)在抛物线上,
∴0=a(3-1)2-2
∴a= ,
,
∴y= (x-1)2-2,
(x-1)2-2,
(2)抛物线与y轴交点B的坐标为(0, ),
),
设直线AB的解析式为y=kx+m,
∴ ,
,
∴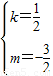 ,
,
∴直线AB的解析式为y= x-
x- .
.
∵P为线段AB上的一个动点,
∴P点坐标为(x, x-
x- ).(0<x<3)
).(0<x<3)
由题意可知PE∥y轴,∴E点坐标为(x, x2-x-
x2-x- ),
),
∵0<x<3,
∴PE=( x-
x- )-(
)-( x2-x-
x2-x- )=-
)=- x2+
x2+ x,
x,
(3)由题意可知D点横坐标为x=1,又D点在直线AB上,
∴D点坐标(1,-1).
①当∠EDP=90°时,△AOB∽△EDP,
∴ .
.
过点D作DQ⊥PE于Q,
∴xQ=xP=x,yQ=-1,
∴△DQP∽△AOB∽△EDP,
∴ ,
,
又OA=3,OB= ,AB=
,AB=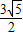 ,
,
又DQ=x-1,
∴DP= (x-1),
(x-1),
∴ ,
,
解得:x=-1± (负值舍去).
(负值舍去).
∴P( -1,
-1, )(如图中的P1点);
)(如图中的P1点);
②当∠DEP=90°时,△AOB∽△DEP,
∴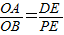 .
.
由(2)PE=- x2+
x2+ x,DE=x-1,
x,DE=x-1,
∴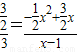 ,
,
解得:x=1± ,(负值舍去).
,(负值舍去).
∴P(1+ ,
, -1)(如图中的P2点);
-1)(如图中的P2点);
综上所述,P点坐标为(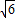 -1,
-1, )或(1+
)或(1+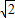 ,
, -1).
-1).
点评:此题考查了待定系数法求函数的解析式,线段的长度的求解方法,相似三角形的判定与性质等知识.此题综合性很强,解题的关键是方程思想,分类讨论思想与数形结合思想的应用.
(2)首先利用待定系数法求得直线AB的解析式,然后由P在直线上,将x代入直线方程,即可求得P的纵坐标,又由E在抛物线上,则可求得E的纵坐标,它们的差即为PE的长;
(3)分别从当∠EDP=90°时,△AOB∽△EDP与当∠DEP=90°时,△AOB∽△DEP两种情况去分析,注意利用相似三角形的对应边成比例等性质,即可求得答案,注意不要漏解.
解答:
 解:(1)设二次函数的解析式为y=a(x-1)2-2,
解:(1)设二次函数的解析式为y=a(x-1)2-2,∵A(3,0)在抛物线上,
∴0=a(3-1)2-2
∴a=
 ,
,∴y=
 (x-1)2-2,
(x-1)2-2,(2)抛物线与y轴交点B的坐标为(0,
 ),
),设直线AB的解析式为y=kx+m,
∴
 ,
,∴
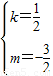 ,
,∴直线AB的解析式为y=
 x-
x- .
.∵P为线段AB上的一个动点,
∴P点坐标为(x,
 x-
x- ).(0<x<3)
).(0<x<3)由题意可知PE∥y轴,∴E点坐标为(x,
 x2-x-
x2-x- ),
),∵0<x<3,
∴PE=(
 x-
x- )-(
)-( x2-x-
x2-x- )=-
)=- x2+
x2+ x,
x,(3)由题意可知D点横坐标为x=1,又D点在直线AB上,
∴D点坐标(1,-1).
①当∠EDP=90°时,△AOB∽△EDP,
∴
 .
.过点D作DQ⊥PE于Q,

∴xQ=xP=x,yQ=-1,
∴△DQP∽△AOB∽△EDP,
∴
 ,
,又OA=3,OB=
 ,AB=
,AB=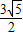 ,
,又DQ=x-1,
∴DP=
 (x-1),
(x-1),∴
 ,
,解得:x=-1±
 (负值舍去).
(负值舍去).∴P(
 -1,
-1, )(如图中的P1点);
)(如图中的P1点);②当∠DEP=90°时,△AOB∽△DEP,
∴
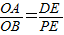 .
.由(2)PE=-
 x2+
x2+ x,DE=x-1,
x,DE=x-1,∴
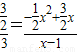 ,
,解得:x=1±
 ,(负值舍去).
,(负值舍去).∴P(1+
 ,
, -1)(如图中的P2点);
-1)(如图中的P2点);综上所述,P点坐标为(
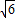 -1,
-1, )或(1+
)或(1+ ,
, -1).
-1).点评:此题考查了待定系数法求函数的解析式,线段的长度的求解方法,相似三角形的判定与性质等知识.此题综合性很强,解题的关键是方程思想,分类讨论思想与数形结合思想的应用.

练习册系列答案
相关题目
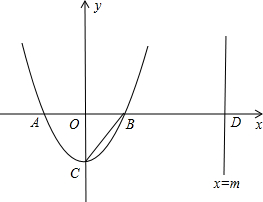 左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.
左边),与y轴交于点C.直线x=m(m>2)与x轴交于点D.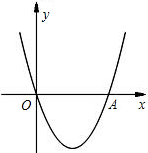 已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.
已知:如图,二次函数y=x2+(2k-1)x+k+1的图象与x轴相交于O、A两点.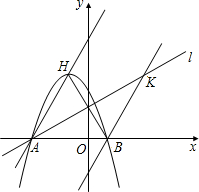 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: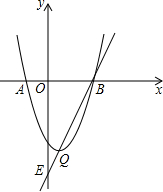 (2013•闸北区一模)已知:如图,二次函数
(2013•闸北区一模)已知:如图,二次函数 已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).
已知:如图,二次函数y=ax2-2ax+c(a≠0)的图象与y轴交于点C(0,4),与x轴交于点A、B,点A的坐标为(4,0).