题目内容
【题目】如果将四根木条首尾相连，在相连处用螺钉连接，就能构成一个平面图形．
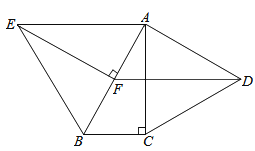
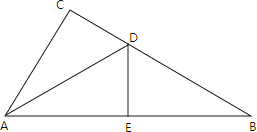
（1）若固定三根木条AB，BC，AD不动，AB=AD=2cm，BC=5cm，如图，量得第四根木条CD=5cm，判断此时∠B与∠D是否相等，并说明理由．
（2）若固定一根木条AB不动，AB=2cm，量得木条CD=5cm，如果木条AD，BC的长度不变，当点D移到BA的延长线上时，点C也在BA的延长线上；当点C移到AB的延长线上时，点A、C、D能构成周长为30cm的三角形，求出木条AD，BC的长度．
【答案】
（1）解：相等．
理由：连接AC，
在△ACD和△ACB中，
，
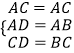∴△ACD≌△ACB，
∴∠B=∠D．
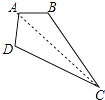
（2）解：设AD=x，BC=y，
当点C在点D右侧时， 
，解得 
，
当点C在点D左侧时， 解得 
，
此时AC=17，CD=5，AD=8，5+8＜17，
∴不合题意，
∴AD=13cm，BC=10cm．
【解析】本题考查全等三角形的判定和性质、二元一次方程组、三角形三边关系定理等知识，解题的关键是学会分类讨论，考虑问题要全面，属于中考常考题型．（1）相等．连接AC，根据SSS证明两个三角形全等即可．（2）分两种情形①当点C在点D右侧时，②当点C在点D左侧时，分别列出方程组即可解决问题，注意最后理由三角形三边关系定理，检验是否符合题意．
练习册系列答案
53随堂测系列答案
相关题目
