��Ŀ����
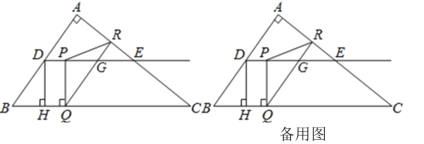
����Ŀ����ͼ����Rt��ABC�У���A=90����AB=6��AC=8��D��E�ֱ��DZ�AB��AC���е㣬��P�ӵ�D������DE�����˶�������P��PQ��BC��Q������Q��QR��BA��AC��R������Q���C�غ�ʱ����Pֹͣ�˶�����BQ=x��QR=y��
(1)���D��BC�ľ���DH�ij���
(2)��y����x�ĺ�����ϵʽ(��Ҫ��д���Ա�����ȡֵ��Χ)��
(3)�Ƿ���ڵ�P��ʹ��PQRΪ����������?�����ڣ��������������Ҫ���x��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��DH=![]() ����2��
����2��![]() ����3�����ڣ�xΪ
����3�����ڣ�xΪ![]() ��
��![]() ��6
��6
��������
��1���������������Ƶ��ж����������BHD�ס�BAC���������������ε��������DH�ij���
��2�����ݡ�RQC�ס�ABC�����������ε����Ʊ����y����x�ĺ�����ϵʽ��
��3������ͼ�Σ�����ͼ�ν������ۣ� PQ��PR�� PQ��RQ�� PR��QR ��
��1����Rt��ABC��
�ߡ�A��90�㣬AB��6��AC��8��
��BC��![]() ��10��
��10��
�ߡ�DHB����A��90�㣬��B����B��
���BHD�ס�BAC��
��![]() ��
��![]() ��
��
��DH��![]() AC��
AC��![]() ��8��
��8��![]()
��2����QR��AB��
���QRC����A��90�㣮
�ߡ�C����C��
���RQC�ס�ABC��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��y����x�ĺ�����ϵʽΪ��y��![]() x+6��
x+6��
��3�����ڣ������������
����PQ��PRʱ������P��PM��QR��M����QM��RM��
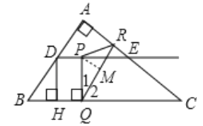
�ߡ�1+��2��90�㣬��C+��2��90�㣬
���1����C��
��cos��1��cosC��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
��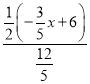 ��
��![]() ��
��
��x��![]() ��
��
����PQ��RQʱ��
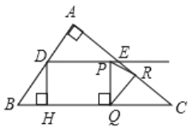
��![]() x+6��
x+6��![]() ��
��
��x��6��
����EM��BC��RN��EM��
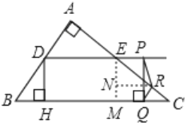
��EM��PQ��
��PR��QRʱ����RΪPQ�д����ϵĵ㣬
��EN��MN��
��ER��RC��
���RΪEC���е㣬
��CR��![]() CE��
CE��![]() AC��2��
AC��2��
��tanC��![]() ��
��![]() ��
��
��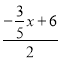 ��
��![]() ��
��
��x��![]() ��
��
������������xΪ![]() ��6��
��6��![]() ʱ����PQRΪ���������Σ�
ʱ����PQRΪ���������Σ�