题目内容
 如图,在⊙O中,弦AB=4
如图,在⊙O中,弦AB=4 cm,圆周角∠ACB=45°,则⊙O的直径是________cm.
cm,圆周角∠ACB=45°,则⊙O的直径是________cm.
8
分析:连接OA和OB,根据同弧所对的圆心角等于圆周角的2倍,由圆周角∠ACB的度数求出圆心角∠AOB的度数为直角,由OA=OB得到三角形AOB为等腰直角三角形,设出OA=OB=xcm,由AB的长,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为⊙O的半径,乘以2即可求出⊙O的直径.
解答: 解:连接OA,OB,
解:连接OA,OB,
∵圆心角∠AOB和圆周角∠ACB所对的弧为 ,又圆周角∠ACB=45°,
,又圆周角∠ACB=45°,
∴圆心角∠AOB=90°,又OA=OB,
∴△AOB为等腰直角三角形,由AB=4 cm,设OA=OB=xcm,
cm,设OA=OB=xcm,
根据勾股定理得:x2+x2=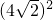 ,解得x=4,
,解得x=4,
∴OA=OB=4cm,
则⊙O的直径是8cm.
故答案为:8.
点评:此题综合考查了圆周角定理、勾股定理以及等腰直角三角形的性质,培养了学生分析问题、解决问题的能力.连接OA和OB构造圆心角∠AOB是本题的突破点.
分析:连接OA和OB,根据同弧所对的圆心角等于圆周角的2倍,由圆周角∠ACB的度数求出圆心角∠AOB的度数为直角,由OA=OB得到三角形AOB为等腰直角三角形,设出OA=OB=xcm,由AB的长,利用勾股定理列出关于x的方程,求出方程的解即可得到x的值,即为⊙O的半径,乘以2即可求出⊙O的直径.
解答:
 解:连接OA,OB,
解:连接OA,OB,∵圆心角∠AOB和圆周角∠ACB所对的弧为
 ,又圆周角∠ACB=45°,
,又圆周角∠ACB=45°,∴圆心角∠AOB=90°,又OA=OB,
∴△AOB为等腰直角三角形,由AB=4
 cm,设OA=OB=xcm,
cm,设OA=OB=xcm,根据勾股定理得:x2+x2=
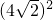 ,解得x=4,
,解得x=4,∴OA=OB=4cm,
则⊙O的直径是8cm.
故答案为:8.
点评:此题综合考查了圆周角定理、勾股定理以及等腰直角三角形的性质,培养了学生分析问题、解决问题的能力.连接OA和OB构造圆心角∠AOB是本题的突破点.

练习册系列答案
相关题目
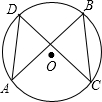 已知:如图,在⊙O中,弦AD=BC.求证:AB=CD.
已知:如图,在⊙O中,弦AD=BC.求证:AB=CD. 4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( )
4、如图,在⊙O中,弦BC∥半径OA,AC与OB相交于M,∠C=20°,则∠AMB的度数为( ) 标系.
标系. 如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( )
如图,在⊙O中,弦AB=BC=CD,且∠ABC=140°,则∠AED=( ) 如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.
如图,在⊙O中,弦AB与CD相交于点P,连接AC、DB.