Question

如图1，△ABC为等腰直角三角形，∠ACB=90°，F是AC边上的一个动点（点F与A、C不重合），以CF为一边在等腰直角三角形外作正方形CDEF，连接BF、AD．

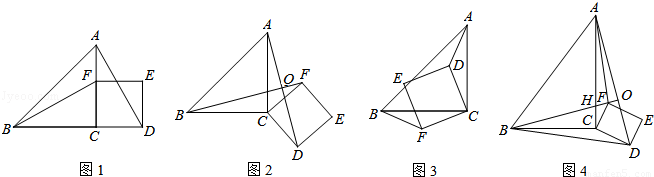
（1）①猜想图1中线段BF、AD的数量关系及所在直线的位置关系，直接写出结论；

②将图1中的正方形CDEF，绕着点C按顺时针（或逆时针）方向旋转任意角度α，得到如图2、图3的情形．图2中BF交AC于点H，交AD于点O，请你判断①中得到的结论是否仍然成立，并选取图2证明你的判断．

（2）将原题中的等腰直角三角形ABC改为直角三角形ABC，∠ACB=90°，正方形CDEF改为矩形CDEF，如图4，且AC=4，BC=3，CD=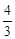，CF=1，BF交AC于点H，交AD于点O，连接BD、AF，求BD²+AF²的值．

 

Answer 1

【答案】

解：（1）①BF=AD，BF⊥AD。

②BF=AD，BF⊥AD仍然成立。证明如下：

∵△ABC是等腰直角三角形，∠ACB=90°，∴AC=BC。

∵四边形CDEF是正方形，∴CD=CF，∠FCD=90°。

∴∠ACB+∠ACF=∠FCD+∠ACF，即∠BCF=∠ACD。

在△BCF和△ACD中，∵BC=AC，∠BCF=∠ACD，CF=CD，

∴△BCF≌△ACD（SAS）。∴BF=AD，∠CBF=∠CAD。

又∵∠BHC=∠AHO，∠CBH+∠BHC=90°，∴∠CAD+∠AHO=90°。∴∠AOH=90°。

∴BF⊥AD。

（2）连接DF，

∵四边形CDEF是矩形，∴∠FCD=90°。

又∵∠ACB=90°，∴∠ACB=∠FCD。

∴∠ACB+∠ACF=∠FCD+∠ACF，即∠BCF=∠ACD。

∵AC=4，BC=3，CD=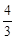，CF=1，

∴B。∴△BCF∽△ACD。∴∠CBF=∠CAD。

又∵∠BHC=∠AHO，∠CBH+∠BHC=90°，∴∠CAD+∠AHO=90°。∴∠AOH=90°。

∴BF⊥AD。∴∠BOD=∠AOB=90°。

∴BD²=OB²+OD²，AF²=OA²+OF²，AB²=OA²+OB²，DF²=OF²+OD²。

∴BD²+AF²=OB²+OD²+OA²+OF²=AB²+DF²。

∵在Rt△ABC中，∠ACB=90°，AC=4，BC=3，∴AB²=AC²+BC²=3²+4²=25。

∵在Rt△FCD中，∠FCD=90°，CD=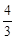，CF=1，∴。

∴。

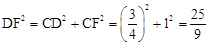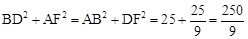【解析】

试题分析：（1）①证△BCF≌△ACD推出∠CAD=∠FBC，BF=AD，即可得出结论。

②证△BCF≌△ACD推出∠CAD=∠FBC，BF=AD，即可得出结论。

（2）连接FD，根据（1）得出BO⊥AD，根据勾股定理得出BD²=OB²+OD²，AF²=OA²+OF²，AB²=OA²+OB²，DF²=OF²+OD²，推出BD²+AF²=AB²+DF²，即可求出答案。