题目内容
5.如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,点D为边BC的中点,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90°.(1)当DP⊥AB时,求CQ的长;
(2)当BP=2,求CQ的长;
(3)连结AD,若AD平分∠PDQ,求DP,DQ的长.
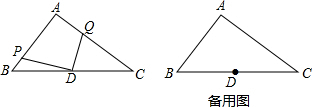
分析 (1)首先证明DQ∥AB,根据平行线等分线段定理即可解决问题.
(2)分两种情形①如图2中,当点P在线段AB上时,作DM⊥AB,DN⊥AC,垂足分别为M、N,由△PDM∽△QDN,得$\frac{PM}{QN}$=$\frac{DM}{DN}$=$\frac{4}{3}$,推出QN=$\frac{3}{4}$PM,推出PM=BM-PB=3-2=1,推出QN=$\frac{3}{4}$即可解决问题.②如图3中,当点P在AB的延长线上时,根据PM=5,QN=$\frac{15}{4}$,CQ=QN+CN计算即可.
(3)如图4中,作AM⊥DP于M,AN⊥DQ于N.首先证明四边形AMDN是正方形,由APM≌△AQN,推出PM=NQ,推出PD+DQ=(PM+MD)+(DN-QN)=2DM=$\sqrt{2}$AD=5$\sqrt{2}$,由(2)可知PD:QD=4:3,由此即可计算.
解答 解:(1)如图1中,
∵DP⊥AB,DQ⊥DP,
∴DQ∥AB,
∵BD=DC,
∴CQ=AQ=4.
(2)①如图2中,当点P在线段AB上时,作DM⊥AB,DN⊥AC,垂足分别为M、N,
则四边形AMDN是矩形,DM、DN分别是△ABC的中位线,DM=4,DN=3,
∵∠PDQ=∠MDN=90°,
∴∠PDM=∠QDN,∵∠DNQ∠DMP=90°,
∴△PDM∽△QDN,
∴$\frac{PM}{QN}$=$\frac{DM}{DN}$=$\frac{4}{3}$,
∴QN=$\frac{3}{4}$PM,
∵PM=BM-PB=3-2=1,
∴QN=$\frac{3}{4}$,
∴CQ=QN+CN=$\frac{3}{4}$+4=$\frac{19}{4}$.
②如图3中,当点P在AB的延长线上时,PM=5,QN=$\frac{15}{4}$,CQ=QN+CN=4+$\frac{15}{4}$=$\frac{31}{4}$,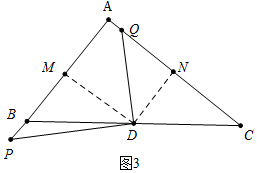
综上所述,当BP=2,求CQ的长为$\frac{19}{4}$或$\frac{31}{4}$.
(3)如图4中,作AM⊥DP于M,AN⊥DQ于N.
∵AD平分∠PDQ,
∴AM=AN,
∵∠AMD=∠AND=∠MDN=90°,
∴四边形AMDN是矩形,∵AM=AN,
∴四边形AMDN是正方形,
∴∠MAN=90°,DM=DN,
∵∠BAC=∠MAN=90°,
∴∠PAM=∠NAQ,
∴△APM≌△AQN,
∴PM=NQ,
∵AB=6,AC=8,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,AD=5,
∵PD+DQ=(PM+MD)+(DN-QN)=2DM=$\sqrt{2}$AD=5$\sqrt{2}$,
由(2)可知PD:QD=4:3,
∴PD=$\frac{4}{7}$×$5\sqrt{2}$=$\frac{20\sqrt{2}}{7}$,QD=$\frac{3}{7}$×5$\sqrt{2}$=$\frac{15\sqrt{2}}{7}$.
点评 本题考查相似三角形综合题、矩形的判定和性质、正方形的判定和性质、三角形的中位线定理、勾股定理等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线构造相似三角形,属于中考压轴题.

| A. | 近似数5.05是精确到0.01的数 | |
| B. | 近似数55.0与55表示的意义是一样的 | |
| C. | 近似数5.05是精确到十分位的数 | |
| D. | 近似数5.05万精确到万位 |

 ,求AB的长.
,求AB的长. 如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题:
如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图象回答下列问题: