题目内容
如图,在直角坐标平面内,O为原点,抛物线y=ax2+bx经过点A(6,0),且顶点B(m,6)在直线y=2x上.(1)求m的值和抛物线y=ax2+bx的解析式;
(2)如在线段OB上有一点C,满足OC=2CB,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请求出点N的坐标.(直接写出结果,不需要过程.)

分析:(1)先根据抛物线y=ax2+bx的顶点B(m,6)在直线y=2x上可求出m的值,再用待定系数发即可求出此抛物线的解析式;
(2)①作CH⊥OA,BG⊥OA,再根据平行线分线段成比例定理即可得出CH的长,进而求出C点坐标,再根据D点坐标用待定系数法即可求出直线DC解析式;
②根据菱形的性质即可求出符合条件的N点坐标.
(2)①作CH⊥OA,BG⊥OA,再根据平行线分线段成比例定理即可得出CH的长,进而求出C点坐标,再根据D点坐标用待定系数法即可求出直线DC解析式;
②根据菱形的性质即可求出符合条件的N点坐标.
解答: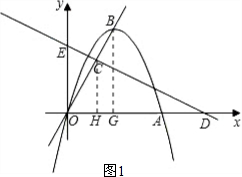 解:(1)∵顶点B(m,6)在直线y=2x,
解:(1)∵顶点B(m,6)在直线y=2x,
∴m=3,(1分)
∴B(3,6),把AB两点坐标代入抛物线的解析式得,
,解得
,
∴抛物线:y=-
x2+4x;(3分)
(2)①如图1,作CH⊥OA,BG⊥OA,
∴CH∥BG,
∴
=
,
∵OC=2CB,
∴
=
,CH=4,
∴点C的坐标为(2,4)(2分)
∵D(10,0)根据题意
,解得:
,
∴直线DC解析式y=-
x+5;(2分)
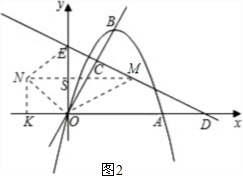
②如图2:∵四边形ENOM是菱形,
∴OS=ES=
OE=
,
∴NK=
,
∵ON∥DE,
∴tan∠NOK=tan∠EDO=
=
=
,
∴OK=5,
∴N1(-5,
),
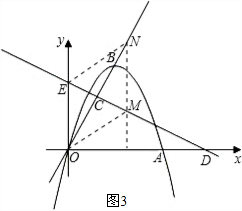
如图3:∵EM⊥OB,
∴ON=2OC,
∵点C的坐标为(2,4),
∴N2(4,8);
③如图4:
∵直线DC解析式y=-
x+5,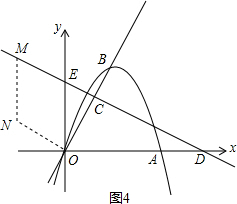
∴E(0,5),
设M(x,-
x+5),
∵四边形ENOM是菱形,
∴EM=OE=5,即x2+(-
x)2=25,解得x=2
,
∴M(-2
,5+
),
∴可设N(-2
,y),则|5+
-y|=5,解得y=
或y=10+
(舍去)
∴N3(-2
,
).
 解:(1)∵顶点B(m,6)在直线y=2x,
解:(1)∵顶点B(m,6)在直线y=2x,∴m=3,(1分)
∴B(3,6),把AB两点坐标代入抛物线的解析式得,
|
|
∴抛物线:y=-
| 2 |
| 3 |
(2)①如图1,作CH⊥OA,BG⊥OA,
∴CH∥BG,
∴
| CH |
| BG |
| OC |
| OB |

∵OC=2CB,
∴
| CH |
| 6 |
| 2 |
| 3 |
∴点C的坐标为(2,4)(2分)
∵D(10,0)根据题意
|
|
∴直线DC解析式y=-
| 1 |
| 2 |
②如图2:∵四边形ENOM是菱形,
∴OS=ES=
| 1 |
| 2 |
| 5 |
| 2 |
∴NK=
| 5 |
| 2 |

∵ON∥DE,
∴tan∠NOK=tan∠EDO=
| EO |
| OD |
| MK |
| OK |
| 1 |
| 2 |
∴OK=5,
∴N1(-5,
| 5 |
| 2 |
如图3:∵EM⊥OB,
∴ON=2OC,
∵点C的坐标为(2,4),
∴N2(4,8);
③如图4:
∵直线DC解析式y=-
| 1 |
| 2 |

∴E(0,5),
设M(x,-
| 1 |
| 2 |
∵四边形ENOM是菱形,
∴EM=OE=5,即x2+(-
| 1 |
| 2 |
| 5 |
∴M(-2
| 5 |
| 5 |
∴可设N(-2
| 5 |
| 5 |
| 5 |
| 5 |
∴N3(-2
| 5 |
| 5 |
点评:本题考查的是二次函数综合题,涉及到用待定系数法求一次函数及二次函数的解析式、菱形的性质、平行线的性质,根据题意作出辅助线是解答此题的关键.

练习册系列答案
相关题目
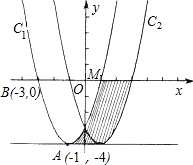 如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)
如图,在直角坐标平面xOy中,抛物线C1的顶点为A(-1,-4),且过点B(-3,0)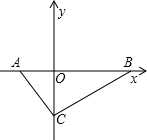 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=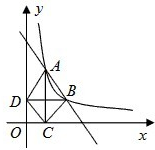 如图,在直角坐标平面内,函数y=
如图,在直角坐标平面内,函数y= 完成下列各题:
完成下列各题: 如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是
如图,在直角坐标平面内的△ABC中,点A的坐标为(0,2),点C的坐标为(5,5),要使以A、B、C、D为顶点的四边形是平行四边形,且点D坐标在第一象限,那么点D的坐标是