题目内容
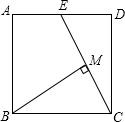如图，正方形ABCD中，E是AD的中点，BM⊥CE，AB=6，则BM=分析：根据正方形的性质，可证△BCM∽△CED，可得
=
，即可求BM的长．
| CD |
| BM |
| CE |
| BC |
解答：解：正方形ABCD中，AB=6，
E是AD的中点，故ED=3；CE=3
，
∵BM⊥CE，
∴△BCM∽△CED，
根据相似三角形的性质，可得
=
，
解得：BM=
．
E是AD的中点，故ED=3；CE=3
| 5 |
∵BM⊥CE，
∴△BCM∽△CED，
根据相似三角形的性质，可得
| CD |
| BM |
| CE |
| BC |
解得：BM=
12
| ||
| 5 |
点评：主要考查了正方形的性质和相似三角形的判定和性质．充分利用正方形的特殊性质来找到相似的条件从而判定相似后利用相似三角形的性质解题．一般情况下求线段的长度常用相似中的比例线段求解．
练习册系列答案
计算高手系列答案
相关题目
19、如图：正方形ABCD，M是线段BC上一点，且不与B、C重合，AE⊥DM于E，CF⊥DM于F．求证：AE2+CF2=AD2．
如图，正方形ABCD中，E点在BC上，AE平分∠BAC．若BE=
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=3．其中正确结论的个数是（ ）
17、如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是
如图，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE、DG．