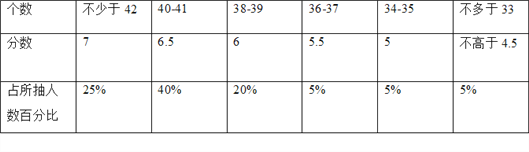
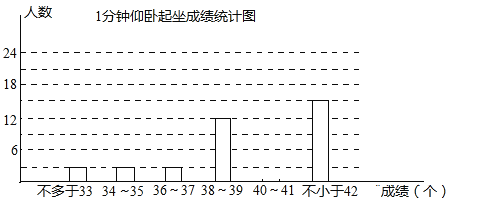
题目内容
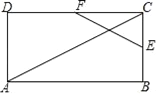
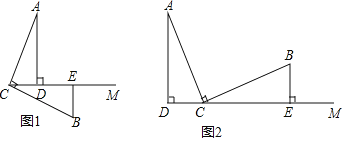
【题目】已知:∠ACB=90°,AC=BC,AD⊥CM,BE⊥CM,垂足分别为D,E,

(1)如图1,
①线段CD和BE的数量关系是 ;
②请写出线段AD,BE,DE之间的数量关系并证明.
(2)如图2,上述结论②还成立吗?如果不成立,请直接写出线段AD,BE,DE之间的数量关系.
【答案】(1)①CD=BE;②AD=BE+DE.证明见解析;(2)②中的结论不成立.DE=AD+BE.
【解析】
(1)①此题可证明出△ACD和△CBE全等即可;②由①全等求解即可;
(2)此时的结论不成立,此时变成DE=AD+BE,依然用△ACD和△CBE全等证明即可.
(1)①CD=BE.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,
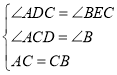 ,
,
∴△ACD≌△CBE,
∴CD=BE.
②AD=BE+DE.
理由:∵△ACD≌△CBE,
∴AD=CE,CD=BE,
∵CE=CD+DE=BE+DE,
∴AD=BE+DE.
(2)②中的结论不成立. DE=AD+BE.
理由:∵AD⊥CM,BE⊥CM,
∴∠ACB=∠BEC=∠ADC=90°,
∴∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠B,
在△ACD和△CBE中,
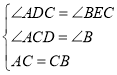 ,
,
∴△ACD≌△CBE,
∴AD=CE,CD=BE,
∵DE=CD+CE=BE+AD,
∴DE=AD+BE.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目