Question

【题目】如图，在矩形ABCD中，已知AB=24，BC=12，点E沿BC边从点B开始向点C以每秒2个单位长度的速度运动；点F沿CD边从点C开始向点D以每秒4个单位长度的速度运动，如果E、F同时出发，用t（0≤t≤6）秒表示运动的时间，当t为何值时，以点E、C、F为顶点的三角形与△ACD相似？

Answer 1

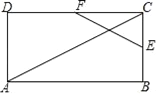
【答案】当t为3或1.2时，以点E，C，F为顶点的三角形与△ACD相似

【解析】试题分析：根据题意可得：EC=12-2t，FC=4t，然后根据和两种情况分别求出t的值，得出答案．

试题解析：根据题意，可分为两种情况：

①若△EFC∽△ACD，则=， 所以=， 解得t=3，

即当t=3时，△EFC∽△ACD．

②若△FEC∽△ACD， 则=， 所以=， 解得t=1.2，

即当t=1.2时，△FEC∽△ACD．

因此，当t为3或1.2时，以点E，C，F为顶点的三角形与△ACD相似．