题目内容
【题目】根据下列要求,解答相关问题.
(1)请补全以下求不等式﹣2x2﹣4x>0的解集的过程.
①构造函数,画出图象:根据不等式特征构造二次函数y=﹣2x2﹣4x;并在下面的坐标系中(图1)画出二次函数y=﹣2x2﹣4x的图象(只画出图象即可).
②求得界点,标示所需,当y=0时,求得方程﹣2x2﹣4x=0的解为 ;并用锯齿线标示出函数y=﹣2x2﹣4x图象中y>0的部分.
③借助图象,写出解集:由所标示图象,可得不等式﹣2x2﹣4x>0的解集为﹣2<x<0.请你利用上面求一元一次不等式解集的过程,求不等式x2﹣2x+1≥4的解集.

【答案】①图见试题解析;②x1=0,x2=﹣2,③不等式的解集是:x≥3或x≤﹣1.
【解析】
试题分析:①利用描点法即可作出函数的图象;
②当y=0时,解方程求得x的值,当y>0时,就是函数图象在x轴上方的部分,据此即可解得;
③仿照上边的例子,首先作出函数y=x2﹣2x+1的图象,然后求得当y=4时对应的x的值,根据图象即可求解.
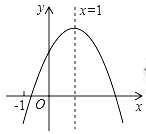
试题解析:①图所示:
 ;
;
②方程﹣2x2﹣4x=0即﹣2x(x+2)=0,
解得:x1=0,x2=﹣2;
则方程的解是x1=0,x2=﹣2,
图象如图1;
③函数y=x2﹣2x+1的图象是:

当y=4时,x2﹣2x+1=4,解得:x1=3,x2=﹣1.
则不等式的解集是:x≥3或x≤﹣1.

练习册系列答案
相关题目
【题目】甲、乙、丙、丁四名射击选手,在相同条件下各射靶10次,他们的成绩统计如下表所示,
若要从他们中挑选一位成绩最高且波动较小的选手参加射击比赛,那么一般应选( )
甲 | 乙 | 丙 | 丁 | |
平均数(环) | 9 | 9.5 | 9 | 9.5 |
方差 | 3.5 | 4 | 4 | 5.4 |
A. 甲 B. 乙 C. 丙 D. 丁