题目内容
【题目】小华的爸爸要用一块矩形铁皮加工出一个底面半径为
，高为
的锥形漏斗，要求只能有一条接缝（接缝忽略不计）
你能求出这个锥形漏斗的侧面展开图的圆心角吗？
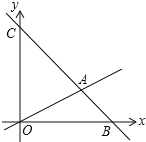
如图，有两种设计方案，请你计算一下，哪种方案所用的矩形铁皮面积较少？
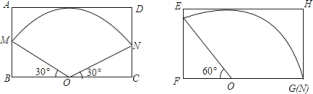
【答案】（1）120°（2）方案二所用的矩形铁皮面积较少
【解析】
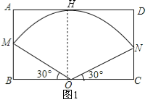
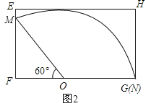
（1）先根据勾股定理求出母线长为60，然后根据圆锥侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长和弧长公式计算锥形漏斗的侧面展开图的圆心角；（2）如图1，矩形的一边长等于母线长60，再利用含30度的直角三角形三边的关系计算出OB，从而得到BC长，再计算矩形ABCD的面积；如图2，矩形的一边长等于母线长60，再利用含30°的直角三角形三边的关系计算出OF，从而得到CG长，再计算矩形EFGH的面积，然后比较两矩形的面积即可．
圆锥的母线长
，
设这个锥形漏斗的侧面展开图的圆心角为
，
所以
，解得
，
即这个锥形漏斗的侧面展开图的圆心角为
；
如图
，
，
，
在
中，∵
，
∴
，
∴
，
∴
，
∴方案一所需的矩形铁皮的面积
，
如图
，
，，
在
中，∵
，
∴
，
∴
，
∴方案二所需的矩形铁皮的面积
，
∴方案二所用的矩形铁皮面积较少．
【题目】某批乒乓球的质量检验结果如下：
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
（1）画出这批乒乓球“优等品”频率的折线统计图；
（2）这批乒乓球“优等品”的概率的估计值是多少？
（3）从这批乒乓球中选择5个黄球、13个黑球、22个红球，它们除颜色外都相同，将它们放入一个不透明的袋中．
①求从袋中摸出一个球是黄球的概率；
②现从袋中取出若干个黑球，并放入相同数量的黄球，搅拌均匀后使从袋中摸出一个是黄球的概率不小于
， 问至少取出了多少个黑球？
