题目内容
如图，已知AD∥BC，AD=BC，AC与BD交于O点，EF过点O并分别交AD、BC于E、F，则图中的全等三角形共有
- A.4对
- B.3对
- C.2对
- D.1对
B
分析：由于AD∥BC，可知∠A=∠C，∠B=∠D，而AD=BC，利用ASA可证△AOD≌△COF，再根据△AOD≌△COF，可知OA=OC，利用一对对顶角和一对内错角相等，利用ASA可证△AOE≌△COF，进而可证△DOE≌△BOF．
解答：△AOD≌△COB，△AOE≌△COF，△DOE≌△BOF，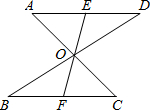
故选B．
点评：本题考查了全等三角形的判定和性质，解题的关键是先证明一对三角形全等，再以此为基础，证明另外三角形的全等．
分析：由于AD∥BC，可知∠A=∠C，∠B=∠D，而AD=BC，利用ASA可证△AOD≌△COF，再根据△AOD≌△COF，可知OA=OC，利用一对对顶角和一对内错角相等，利用ASA可证△AOE≌△COF，进而可证△DOE≌△BOF．
解答：△AOD≌△COB，△AOE≌△COF，△DOE≌△BOF，
故选B．
点评：本题考查了全等三角形的判定和性质，解题的关键是先证明一对三角形全等，再以此为基础，证明另外三角形的全等．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
9、如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠ABC=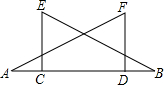
如图，已知AD=BC．EC⊥AB．DF⊥AB，C．D为垂足，要使△AFD≌△BEC，还需添加一个条件．若以“ASA”为依据，则添加的条件是
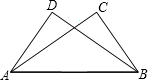如图，已知AD=BC，AC=BD，∠DAC与∠CBD有什么关系？说说你的理由．
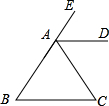如图，已知AD∥BC，AD平分∠CAE，试说明△ABC是等腰三角形．
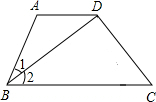如图，已知AD∥BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠C=