题目内容
如图所示,在Rt△ABC中,∠C=90°,∠A=60°,AB=12cm,若点P从B点出发以2cm/秒的速度向A点运动,点Q从A点出发以1cm/秒的速度向C点运动,设P、Q分别从B、A同时出发,运动时间为![]() 秒,解答下列问题:
秒,解答下列问题:
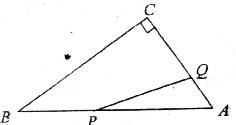
(1)用含![]() 的代数式表示线段AP,AQ的长;
的代数式表示线段AP,AQ的长;
(2)当![]() 为何值时△APQ是以PQ为底的等腰三角形?
为何值时△APQ是以PQ为底的等腰三角形?
(3)当![]() 为何值时PQ//BC?
为何值时PQ//BC?
解:由已知条件易知AC=6cm,BP=2t,AP=12-2t,AQ=t,
(2)由AP=AQ,即l2-2t=t,得t=4,即当t=4秒时△PCQ是等腰三角形;
(3)若PQ//BD,则AQ:AC=AP:AB,即t:6=(12-2):12,解得t=3,即当t=3秒时,PQ//BD。

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
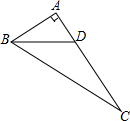 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB= 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE. 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB= 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.