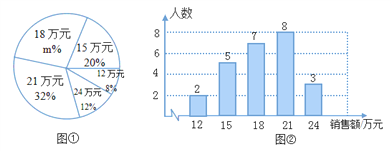
题目内容
【题目】如图,在△ABC中,AB=5,AC=4,∠A=60°,若边AC的垂直平分线DE交AB于点D,连接CD,
求(1)BC的长;
(2)△BDC的周长.
【答案】(1)![]() ;(2)△BDC的周长是5+
;(2)△BDC的周长是5+![]()
【解析】
(1)过点C作CM⊥AB,在Rt△AMC中,由特殊的∠A得到CM、AM的长,在Rt△BMC中,利用勾股定理求出线段BC的长;
(2)根据线段垂直平分线的性质可得到AD=CD,又∠A=60°,那么△ACD是等边三角形,CD=AD=AC=4,再通过等量代换得到△BDC的周长=BC+BD+CD=BC+AB,即可求解.
(1)过点C作CM⊥AB,垂足为M.
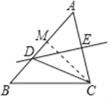
在Rt△AMC中,∵∠A=60°,AC=4,
∴AM=2,MC=2![]() ,
,
∴BM=AB﹣AM=3.
在Rt△BMC中,
BC=![]() =
=![]() =
=![]() .
.
(2)∵DE是线段AC的垂直平分线,
∴AD=DC,又∵∠A=60°,
∴△ADC是等边三角形
∴CD=AD=AC=4
∴L△BDC=DB+DC+BC=AD+DB+BC=AB+BC=5+![]() .
.
即△BDC的周长是5+![]() .
.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目