题目内容
如图,AB为⊙O直径,CD为弦,且CD⊥AB,垂足为H.
(1)∠OCD的平分线CE交⊙O于E,连接OE.求证:E为
的中点;
(2)如果⊙O的半径为1,CD=
.
①求O到弦AC的距离;
②填空:此时圆周上存在______个点到直线AC的距离为
.

(1)∠OCD的平分线CE交⊙O于E,连接OE.求证:E为
 |
| ADB |
(2)如果⊙O的半径为1,CD=
| 3 |
①求O到弦AC的距离;
②填空:此时圆周上存在______个点到直线AC的距离为
| 1 |
| 2 |

(1)证明:∵OC=OE
∴∠E=∠OCE(1分)
又∠OCE=∠DCE
∴∠E=∠DCE
∴OE∥CD(2分)
又OE⊥AB
∴∠AOE=∠BOE=90°
∴E为
的中点;(3分)
(2)①∵CD⊥AB,AB为⊙O的直径,CD=
∴CH=
CD=
(4分)
又OC=1
∴sin∠COB=
=
=
∴∠COB=60°(5分)
∴∠BAC=30°
作OP⊥AC于P,则OP=
OA=
;(6分)
②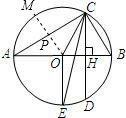 OP=
OP=
,则MP=
,即M到AC的距离是
,在
上其它点到AC的距离一定小于
;
在
上一定有2个点到AC的距离等于
.
故圆上有3点到AC的距离是
.
故答案是:3.(7分)
∴∠E=∠OCE(1分)
又∠OCE=∠DCE
∴∠E=∠DCE
∴OE∥CD(2分)
又OE⊥AB
∴∠AOE=∠BOE=90°
∴E为
 |
| ADB |
(2)①∵CD⊥AB,AB为⊙O的直径,CD=
| 3 |
∴CH=
| 1 |
| 2 |
| ||
| 2 |
又OC=1
∴sin∠COB=
| CH |
| OC |
| ||||
| 1 |
| ||
| 2 |
∴∠COB=60°(5分)
∴∠BAC=30°
作OP⊥AC于P,则OP=
| 1 |
| 2 |
| 1 |
| 2 |
②
 OP=
OP=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 |
| AC |
| 1 |
| 2 |
在
 |
| ADB |
| 1 |
| 2 |
故圆上有3点到AC的距离是
| 1 |
| 2 |
故答案是:3.(7分)

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目






