题目内容
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B. C重合),以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC.设∠BAC=α,∠BCE=β.

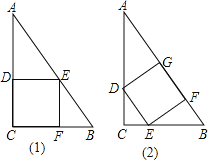
(1)如图1,如果∠BAC=90,∠BCE=___度;
(2)如图2,你认为α、β之间有怎样的数量关系?并说明理由。
(3)当点D在线段BC的延长线上移动时,α、β之间又有怎样的数量关系?请在备用图上画出图形,并直接写出你的结论。
【答案】(1)90°;(2)α+β=180°,理由见解析;(3)α+β=180°,理由见解析
【解析】
(1)根据题干中给出的条件可以证明△ABD≌△ACE,即可证明∠B=∠ACE,即可求出∠BCE的度数;
(2)根据(1)中的△ABD≌△ACE,可以证明α+β=180°;
(3)连接AD,作AE使得∠DAE=∠BAC,AE=AD,连接DE、CE,可得△ABD≌△ACE(SAS),即可证明:α+β=180°.
(1)∵∠DAE=∠BAC,∠BAC=∠BAD+∠DAC,∠DAE=∠EAC+∠DAC;
∴∠CAE=∠BAD;
在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180∠BAC=90°;
(2)由(1)中可知β=180°α,
∴α、β存在的数量关系为α+β=180°;
(3)连接AD,作AE使得∠DAE=∠BAC,AE=AD,连接DE、CE,可得下图:

∵∠BAD=∠BAC+∠CAD,∠CAE=∠DAE+∠CAD,∴∠BAD=∠CAE;
在△ABD和△ACE中,

∴△ABD≌△ACE(SAS);
∴∠B=∠ACE;
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°∠BAC.
∴α、β存在的数量关系为α+β=180°;