题目内容
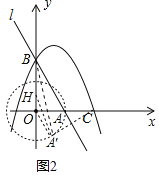
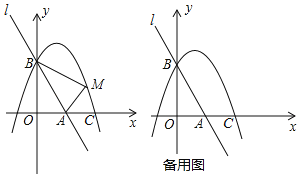
【题目】如图，直线l：y＝﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y＝ax2﹣2ax+a+4（a＜0）经过点B，交x轴正半轴于点C．
（1）求该抛物线的函数表达式；
（2）已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值及此时动点M的坐标；
（3）将点A绕原点旋转得点A′，连接CA′、BA′，在旋转过程中，一动点M从点B出发，沿线段BA′以每秒3个单位的速度运动到A′，再沿线段A′C以每秒1个单位长度的速度运动到C后停止，求点M在整个运动过程中用时最少是多少？
【答案】（1）y＝﹣x2+2x+3；（2）S与m的函数表达式是S＝
，S的最大值是
，此时动点M的坐标是（
，
）；（3）点M在整个运动过程中用时最少是
秒．
【解析】
（1）首先求出B点的坐标，根据B点的坐标即可计算出二次函数的a值，进而即可计算出二次函数的解析式;
（2）计算出C点的坐标，设出M点的坐标，再根据△ABM的面积为S＝S四边形OAMB﹣S△AOB＝S△BOM+S△OAM﹣S△AOB，化简成二次函数，再根据二次函数求解最大值即可.
（3）首先证明△OHA′∽△OA′B，再结合A′H+A′C≥HC即可计算出t的最小值.
（1）将x＝0代入y＝﹣3x+3，得y＝3，
∴点B的坐标为（0，3），
∵抛物线y＝ax2﹣2ax+a+4（a＜0）经过点B，
∴3＝a+4，得a＝﹣1，
∴抛物线的解析式为：y＝﹣x2+2x+3；
（2）将y＝0代入y＝﹣x2+2x+3，得x1＝﹣1，x2＝3，
∴点C的坐标为（3，0），
∵点M是抛物线上的一个动点，并且点M在第一象限内，点M的横坐标为m，
∴0＜m＜3，点M的坐标为（m，﹣m2+2m+3），
将y＝0代入y＝﹣3x+3，得x＝1，
∴点A的坐标（1，0），
∵△ABM的面积为S，
∴S＝S四边形OAMB﹣S△AOB＝S△BOM+S△OAM﹣S△AOB＝
，
化简，得
S＝＝
，
∴当m＝时，S取得最大值，此时S＝，此时点M的坐标为（，），
即S与m的函数表达式是S＝，S的最大值是，此时动点M的坐标是（，）；
（3）如右图所示，取点H的坐标为（0，
），连接HA′、OA′，
∵∠HOA′＝∠A′OB，
，
，
∴△OHA′∽△OA′B，
∴
，
即
，
∵A′H+A′C≥HC＝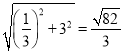
，
∴t≥，
即点M在整个运动过程中用时最少是秒．
