题目内容
【题目】我们定义一种新函数:形如![]() (
(![]() ,且
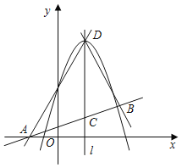
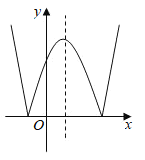
,且![]() )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|
)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2-2x-3|![]() 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为
的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为![]() ,
,![]() 和
和![]() ;②图象具有对称性,对称轴是直线
;②图象具有对称性,对称轴是直线![]() ;③当
;③当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 或
或![]() 时,函数的最小值是0;⑤当
时,函数的最小值是0;⑤当![]() 时,函数的最大值是4.其中正确结论的个数是______.
时,函数的最大值是4.其中正确结论的个数是______.
【答案】4
【解析】
由![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线
,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,②也是正确的;
,②也是正确的;
根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;函数图象的最低点就是与
值的增大而增大,因此③也是正确的;函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;从图象上看,当
,因此④也是正确的;从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;逐个判断之后,可得出答案.
,因此⑤时不正确的;逐个判断之后,可得出答案.
解:①∵![]() ,
,![]() 和
和![]() 坐标都满足函数
坐标都满足函数![]() ,∴①是正确的;
,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线![]() ,因此②也是正确的;
,因此②也是正确的;
③根据函数的图象和性质,发现当![]() 或
或![]() 时,函数值
时,函数值![]() 随
随![]() 值的增大而增大,因此③也是正确的;
值的增大而增大,因此③也是正确的;
④函数图象的最低点就是与![]() 轴的两个交点,根据
轴的两个交点,根据![]() ,求出相应的
,求出相应的![]() 的值为
的值为![]() 或
或![]() ,因此④也是正确的;
,因此④也是正确的;
⑤从图象上看,当![]() 或
或![]() ,函数值要大于当
,函数值要大于当![]() 时的
时的![]() ,因此⑤时不正确的;
,因此⑤时不正确的;
故答案是:4
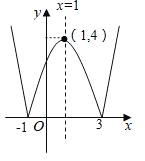

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目