题目内容
如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A坐标为(1,3),A、B两点关于直线y=x对称,反比例函数y=
(x>0)图象经过点A,点P是直线y=x上一动点.
(1)B点的坐标为 ;
(2)若点C是反比例函数图象上一点,是否存在这样的点C,使得以A、B、C、P四点为顶点的四边形是平行四边形?若存在,求出点C坐标;若不存在,请说明理由;
(3)若点Q是线段OP上一点(Q不与O、P重合),当四边形AOBP为菱形时,过点Q分别作直线OA和直线AP的垂线,垂足分别为E、F,当QE+QF+QB的值最小时,求出Q点坐标.

| k |
| x |
(1)B点的坐标为
(2)若点C是反比例函数图象上一点,是否存在这样的点C,使得以A、B、C、P四点为顶点的四边形是平行四边形?若存在,求出点C坐标;若不存在,请说明理由;
(3)若点Q是线段OP上一点(Q不与O、P重合),当四边形AOBP为菱形时,过点Q分别作直线OA和直线AP的垂线,垂足分别为E、F,当QE+QF+QB的值最小时,求出Q点坐标.

考点:反比例函数综合题
专题:动点型,分类讨论
分析:(1)根据点(a,b)关于y=x对称的点的坐标为(b,a)直接写出答案即可;
(2)首先求得反比例函数的解析式,然后设P(m,m),分若PC为平行四边形的边和若PC为平行四边形的对角线两种情况分类讨论即可确定点C的坐标;
(3)连接AQ,设AB与PO的交点为D,利用四边形AOBP是菱形,得到S△AOP=S△AOQ+S△APQ,从而得到
PO•AD=
AO•QE+
AP•QF,确定QE+QF=
为定值,从而求解.
(2)首先求得反比例函数的解析式,然后设P(m,m),分若PC为平行四边形的边和若PC为平行四边形的对角线两种情况分类讨论即可确定点C的坐标;
(3)连接AQ,设AB与PO的交点为D,利用四边形AOBP是菱形,得到S△AOP=S△AOQ+S△APQ,从而得到
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| PO•AD |
| AO |
解答: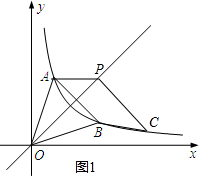 解:(1)B点的坐标为(3,1);
解:(1)B点的坐标为(3,1);
(2)∵反比例函数y=
(x>0)图象经过点A(1,3),
∴k=1×3=3,
∴反比例函数的解析式为y=
,
∵点P在直线y=x上,
∴设P(m,m)
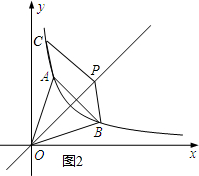 ①若PC为平行四边形的边,
①若PC为平行四边形的边,
∵点A的横坐标比点B的横坐标小2,点A的纵坐标比点B的纵坐标大2,
∴点C在点P的下方,则点C的坐标为(m+2,m-2)如图1,
若点C在点P的上方,则点C的坐标为(m-2,m+2)如图2,
把C(m+2,m-2)代入反比例函数的解析式得:m=±
,
∵m>0,
∴m=
,>
∴C1(
+2,
-2),
 同理可得另一点C2(
同理可得另一点C2(
-2,
+2);
②若PC为平行四边形的对角线,如图3,
∵A、B关于y=x对称,
∴OP⊥AB
此时点C在直线y=x上,且为直线y=x与双曲线y=
的交点,
由
解得
,
(舍去)
∴C3(
,
)
综上所述,满足条件的点C有三个,坐标分别为:C1(
+2,
-2),C2(
-2,
+2),C3(
,
);
 (3)连接AQ,设AB与PO的交点为D,如图4,
(3)连接AQ,设AB与PO的交点为D,如图4,
∵四边形AOBP是菱形,
∴AO=AP
∵S△AOP=S△AOQ+S△APQ,
∴
PO•AD=
AO•QE+
AP•QF
∴QE+QF=
为定值,
∴要使QE+QF+QB的值最小,只需QB的值当QB⊥PO时,QB最小,
所以D点即为所求的点,
∵A(1,3),B(3,1)
∴D(2,2),
∴当QE+QF+QB的值最小时,Q点坐标为(2,2).
 解:(1)B点的坐标为(3,1);
解:(1)B点的坐标为(3,1);(2)∵反比例函数y=
| k |
| x |
∴k=1×3=3,
∴反比例函数的解析式为y=
| 3 |
| x |
∵点P在直线y=x上,
∴设P(m,m)
 ①若PC为平行四边形的边,
①若PC为平行四边形的边,∵点A的横坐标比点B的横坐标小2,点A的纵坐标比点B的纵坐标大2,
∴点C在点P的下方,则点C的坐标为(m+2,m-2)如图1,
若点C在点P的上方,则点C的坐标为(m-2,m+2)如图2,
把C(m+2,m-2)代入反比例函数的解析式得:m=±
| 7 |
∵m>0,
∴m=
| 7 |
∴C1(
| 7 |
| 7 |
 同理可得另一点C2(
同理可得另一点C2(| 7 |
| 7 |
②若PC为平行四边形的对角线,如图3,
∵A、B关于y=x对称,
∴OP⊥AB
此时点C在直线y=x上,且为直线y=x与双曲线y=
| 3 |
| x |
由
|
解得
|
|
∴C3(
| 3 |
| 3 |
综上所述,满足条件的点C有三个,坐标分别为:C1(
| 7 |
| 7 |
| 7 |
| 7 |
| 3 |
| 3 |
 (3)连接AQ,设AB与PO的交点为D,如图4,
(3)连接AQ,设AB与PO的交点为D,如图4,∵四边形AOBP是菱形,
∴AO=AP
∵S△AOP=S△AOQ+S△APQ,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴QE+QF=
| PO•AD |
| AO |
∴要使QE+QF+QB的值最小,只需QB的值当QB⊥PO时,QB最小,
所以D点即为所求的点,
∵A(1,3),B(3,1)
∴D(2,2),
∴当QE+QF+QB的值最小时,Q点坐标为(2,2).
点评:本题考查了反比例函数的综合知识,本题中涉及了分类讨论的数学思想,难度较大,这也是中考的热点题型之一.

练习册系列答案
相关题目
 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点O,与BC相交于N,连接BM,DN. 已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE、DE交于点E.求证:四边形DOAE是菱形.
已知:如图,矩形ABCD的对角线相交于点O,DE∥AC,AE∥DB,AE、DE交于点E.求证:四边形DOAE是菱形. 在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0).
在如图所示的平面直角坐标系中描出下面各点:A(0,3);B(1,-3);C(3,-5);D(-3,-5);E(3,5);F(5,7);G(5,0). 如图,平行四边形ABCD中,O是对角线AC的中点,EF⊥AC交CD于E,交AB于F,问四边形AFCE是菱形吗?请说明理由.
如图,平行四边形ABCD中,O是对角线AC的中点,EF⊥AC交CD于E,交AB于F,问四边形AFCE是菱形吗?请说明理由.