题目内容
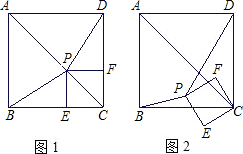
如图1,已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.(1)试说明:BP=DP;
(2)如图2,若正方形PECF绕点C按逆时针方向旋转,在旋转过程中是否总有BP=DP?若是,请给予证明;若不是,请画图用反例加以说明;
(3)试选取正方形ABCD的两个顶点,分别与正方形PECF的两个顶点连接,使得到的两条线段在正方形PECF绕点C按逆时针方向旋转的过程中长度始终相等,并证明你的结论;
(4)旋转的过程中AP和DF的长度是否相等?若不等,直接写出AP:DF=
(5)若正方形ABCD的边长是4,正方形PECF的边长是1.把正方形PECF绕点C按逆时针方向旋转
 的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
的过程中,△PBD的面积是否存在最大值、最小值?如果存在,试求出最大值、最小值;如果不存在,请说明理由.
分析:(1)求简单的相等,可证线段所在的三角形全等,即证△ADP≌△ABP即可.
(2)显然BP、PD不会总是相等,例如:当P不在直线AC上时,连接AP,显然∠BAP≠∠DAP,那么△BAP、△DAP不全等,因此BP、PD不会相等.
(3)此题较简单,例如选线段DF、BE,当P位于直线AC上时,显然两者相等;若P不位于直线AC上时,可通过证△BCE≌△DCF来证得所求的结论.
(4)AP、DF显然不相等,图2中,连接AP,证△APC∽△DFC即可.
(5)连接BD,由于BD是定值,那么△PBD面积的大小与P到直线BD的距离有关;因此当△BPD得面积最小或最大时,点P都位于直线AC上,可据此求解.
(2)显然BP、PD不会总是相等,例如:当P不在直线AC上时,连接AP,显然∠BAP≠∠DAP,那么△BAP、△DAP不全等,因此BP、PD不会相等.
(3)此题较简单,例如选线段DF、BE,当P位于直线AC上时,显然两者相等;若P不位于直线AC上时,可通过证△BCE≌△DCF来证得所求的结论.
(4)AP、DF显然不相等,图2中,连接AP,证△APC∽△DFC即可.
(5)连接BD,由于BD是定值,那么△PBD面积的大小与P到直线BD的距离有关;因此当△BPD得面积最小或最大时,点P都位于直线AC上,可据此求解.
解答:解:(1)证明:如图1;
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°;
又∵AP=AP,
∴△BAP≌△DAP,
∴BP=PD.
(2)BP、PD不会总相等;理由如下: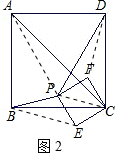
如图2,连接AP;
当P不在直线AC上时,∠BAP≠∠DAP,
∴△BAP与△DAP不全等,故BP≠PD.
(3)选连接DF、BE;
证明:①当P在线段AC上时,由于CF=CE,BC=CD;
则DF=BE=BC-CE=CD-CF;
②当P不在直线AC上时,连接BE、DF;
∵BC=CD、CF=CE、∠BCE=∠DCF(旋转角),
∴△DCF≌△BCE,即BE=DF;
③当P在线段AC的延长线上时,证法同①;
综上可知:连接DF、BE,则DF、BE的长总相等.
(4)连接AP、PC;
∵四边形ABCD、四边形CFPE都是正方形,
∴
=
=
;
又∵∠ACP=∠DCF=45°-∠ACF,
∴△ACP∽△DCF,得:AP:DF=
:1.
(5)连接BD,由于BD是定值,而P到直线BD的距离随正方形FPEC的旋转而改变,因此△PBD的面积不是定值;
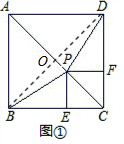
①如图①,当P在线段AC上时,P到直线BD的距离最小,此时△PBD的面积最小;
易知:OC=2
,PC=
,则OP=OC-PC=
;
∴△PBD的面积:Smin=
×BD×OP=
×4
×
=4;
②如图②,当P在线段AC的延长线上时,P到直线BD的距离最大,此时△PBD的面积最大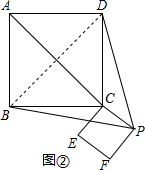
易知此时:OP=OC+CP=3
;
∴△PBD的面积:Smax=
×BD×OP=
×4
×3
=12.
综上可知:△PBD的面积存在最大和最小值;
且最大值为12,最小值为4.
∵四边形ABCD是正方形,
∴AB=AD,∠BAP=∠DAP=45°;
又∵AP=AP,
∴△BAP≌△DAP,
∴BP=PD.
(2)BP、PD不会总相等;理由如下:

如图2,连接AP;
当P不在直线AC上时,∠BAP≠∠DAP,
∴△BAP与△DAP不全等,故BP≠PD.
(3)选连接DF、BE;
证明:①当P在线段AC上时,由于CF=CE,BC=CD;
则DF=BE=BC-CE=CD-CF;
②当P不在直线AC上时,连接BE、DF;
∵BC=CD、CF=CE、∠BCE=∠DCF(旋转角),
∴△DCF≌△BCE,即BE=DF;
③当P在线段AC的延长线上时,证法同①;
综上可知:连接DF、BE,则DF、BE的长总相等.
(4)连接AP、PC;
∵四边形ABCD、四边形CFPE都是正方形,
∴
| CF |
| CP |
| CD |
| AC |
| 1 | ||
|
又∵∠ACP=∠DCF=45°-∠ACF,
∴△ACP∽△DCF,得:AP:DF=
| 2 |
(5)连接BD,由于BD是定值,而P到直线BD的距离随正方形FPEC的旋转而改变,因此△PBD的面积不是定值;
①如图①,当P在线段AC上时,P到直线BD的距离最小,此时△PBD的面积最小;
易知:OC=2
| 2 |
| 2 |
| 2 |
∴△PBD的面积:Smin=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
②如图②,当P在线段AC的延长线上时,P到直线BD的距离最大,此时△PBD的面积最大


易知此时:OP=OC+CP=3
| 2 |
∴△PBD的面积:Smax=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
综上可知:△PBD的面积存在最大和最小值;
且最大值为12,最小值为4.
点评:此题主要考查了正方形的性质、图形的旋转变化、全等三角形及相似三角形的判定和性质、三角形面积的计算方法等知识的综合应用能力,难度较大.

练习册系列答案
相关题目
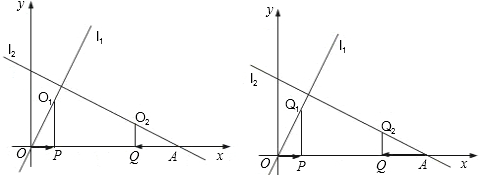 ,求出t值;若不能,说明理由.(同学可在图2中画草图)
,求出t值;若不能,说明理由.(同学可在图2中画草图)