题目内容
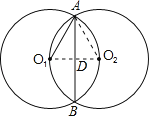
【题目】如图,等圆⊙O1、⊙O2相交于AB,圆心O1、O2分别在另一个圆上
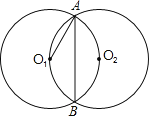
(1)求∠O1AB的大小;
(2)若圆的半径为2cm,求公共弦AB的长.
【答案】(1)∠O1AB=30°;(2)AB=2![]() .
.
【解析】
(1)连接AO2,O1O2,设AB交O1O2于点D,由于两圆为等圆可得出AO1=AO2=O1O2,进而可得出△AO1O2为等边三角形,利用等边三角形的性质可得出∠O1AO2=60°,利用相交两圆的性质可得出O1O2⊥AB,利用等腰三角形的三线合一可得出BA平分∠O1AO2,进而可求出∠O1AB的大小;
(2)在Rt△O1AD中,通过解直角三角形可求出AD的长,由O1O2⊥AB利用垂径定理可得出AB=2AD=2![]() ,此题得解.
,此题得解.
解:(1)连接AO2,O1O2,设AB交O1O2于点D,如图所示.
∵⊙O1、⊙O2为等圆,
∴AO1=AO2=O1O2,
∴△AO1O2为等边三角形,
∴∠O1AO2=60°.
又∵O1O2⊥AB,
∴BA平分∠O1AO2,
∴∠O1AB=![]() ∠O1AO2=30°.
∠O1AO2=30°.
(2)在Rt△O1AD中,O1A=2,∠O1AD=30°,
∴AD=O1Acos∠O1AD=![]() .
.
∵O1O2⊥AB,
∴AB=2AD=2![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目