题目内容
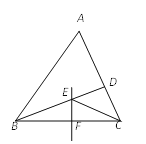
【题目】如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
(1)∠GAF等于多少度?为什么?
(2)EF与FG相等吗?为什么?
(3)△AEF与△AGF有何种位置关系?

【答案】解:(1)∠GAF=45°;(2)EF=FG;(3)△AEF与△AGF关于直线AF轴对称.
【解析】
(1)由旋转的性质可知△ADE≌△ABG,可知AE=AG,∠DAE=∠BAG,故∠GAF=∠GAB+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF;
(2)由(1)可知∠EAF=∠GAF,且AE=AG,AF=AF,可证△AEF≌△AGF,从而得EF=FG;
(3)根据(2)可知△AEF≌△AGF.
解:(1)∠GAF=45°.
∵△ABG是将△ADE绕A点顺时针旋转90°得到的,
∴∠DAE=∠BAG,
∵∠EAF=45°,∠BAD=90°,
∴∠DAE+∠FAB=90°﹣45°=45°,
∴∠BAG+∠FAB=45°,即∠GAF=45°;
(2)EF=FG.
理由:∵△ABG是△ADE旋转90°得到的,
∴AE=AG,
∵∠EAF=45°,∠GAF=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,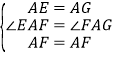 ,
,
∴△AEF≌△AGF,
∴EF=FG;
(3)△AEF与△AGF关于直线AF轴对称.
由△AEF≌△AGF易证.

练习册系列答案
相关题目