题目内容
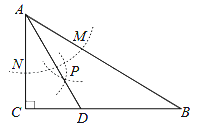
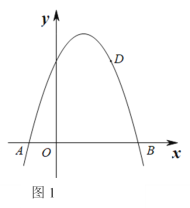
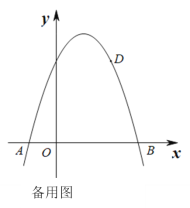
【题目】如图1,抛物线y=ax2+bx +3与x轴的交点为A和B,其中点A(-1,0),且点D(2,3)在该抛物线上.
(1)求该抛物线所对应的函数解析式;
(2)点P是线段AB上的动点(点P不与点A,B重合),过点P作PQ⊥x轴交该抛物线于点Q,连接AQ,DQ,记点P的横坐标为t.
①若![]() 时,求△
时,求△![]() 面积的最大值;
面积的最大值;
②若△![]() 是以Q为直角顶点的直角三角形时,求所有满足条件的点Q的坐标.
是以Q为直角顶点的直角三角形时,求所有满足条件的点Q的坐标.
【答案】(1)![]() ;(2)①当
;(2)①当![]() 时,△ADQ面积最大为
时,△ADQ面积最大为![]() ;②Q(
;②Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)把A(-1,0),D(2,3)代入解析式即可求解;
(2)①由P的横坐标为t, Q(t,![]() ),求出直线AD的解析式为
),求出直线AD的解析式为![]() ,设点C为直线PQ与直线AD的交点,求得点
,设点C为直线PQ与直线AD的交点,求得点![]() 坐标为(
坐标为(![]() ),得到
),得到![]()
![]() ,利用
,利用![]() ,将△
,将△![]() 面积表示为关于t的二次函数,故可求解;
面积表示为关于t的二次函数,故可求解;
②△AQD是以Q为直角顶点的直角三角形时,∠AQD=90°,过点D作DK⊥PQ于点K,
证明△PQA∽△KDQ得到![]() ,代入得
,代入得![]() ,解出t即可求解.
,解出t即可求解.
(1)解:将A(-1,0)和点D(2,3)代入![]() 得,
得,
![]() ,
,
解得![]() ,
,
∴该抛物线的解析式为![]() .
.
(2)①由P的横坐标为t,则P(t,0),Q(t,![]() ).
).
设直线AD的解析式为y=kx+b(k≠0)
把A(-1,0),D(2,3)代入得![]()
解得![]()
∴直线AD的解析式为![]()
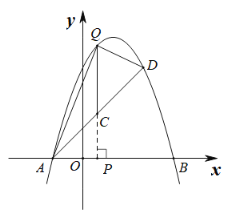
如图:设点C为直线PQ与直线AD的交点
当![]() 时,
时,![]()
∴点![]() 坐标为(
坐标为(![]() )
)
∴![]()
![]()
∴![]()
![]()
![]()
![]()
![]()
![]()
![]() 抛物线开口向下
抛物线开口向下
∴当![]() 时,△ADQ面积最大为
时,△ADQ面积最大为![]() ;
;
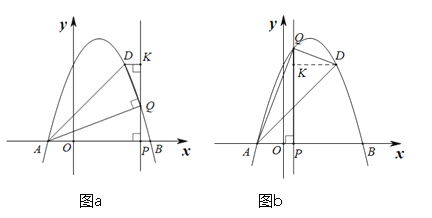
②△AQD是以Q为直角顶点的直角三角形时,∠AQD=90°,
过点D作DK⊥PQ于点K,
∴∠APQ=∠QKD=90°,
∵∠DQK+∠PQA=90°,
又∠DQK+∠KDQ=90°,
∴∠PQA=∠KDQ,
∴△PQA∽△KDQ
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() (即Q不与A、D重合),
(即Q不与A、D重合),
∴![]() ,整理得:
,整理得:![]() ,
,
解得![]() ,
,![]()
经验证,![]() 、
、![]() 均符合题意,
均符合题意,
其中:![]() ,符合图a的情况,
,符合图a的情况,![]() ,符合图b的情况.
,符合图b的情况.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴Q(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
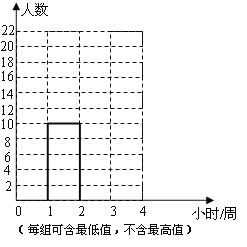
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?