题目内容
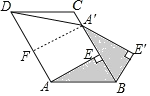
【题目】如图,已知在ABCD中,AE⊥BC于点E,以点B为中心,取旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,连接DA′.若∠ADC=60°,AD=5,DC=4,则DA′的大小为( )

A. 1 B. ![]() C.
C. ![]() D. 2
D. 2![]()
【答案】C
【解析】
过A′作A′F⊥AD,由AE⊥BC可得AE=A′F,根据平行四边形的性质可知AB=CD=4,∠ABC=∠ADC=60°,进而可求出BE和AE的长,根据旋转的性质可得AB=A′B,进而可求出A′E的长,即可求出AF的长,进而求出DF的长,利用勾股定理求出DA′的长即可.
如图:过A′作A′F⊥AD,
∵四边形ABCD为平行四边形,AE⊥BC,A′F⊥AD,
∴AE=A′F,
∵四边形ABCD为平行四边形,
∴AB=CD=4,∠ABC=∠ADC=60°,
∴∠BAE=30°,
∴BE=![]() AB=2,AE=A′F=
AB=2,AE=A′F=![]() =2
=2![]() ,
,
∵旋转角等于∠ABC,把△BAE顺时针旋转,得到△BA′E′,
∴A′B在线段BC上,且A′B=AB=5,
∴A′E=A′B-BE=5-2=3,
∴AF=A′E=3,
∴DF=DA-AF=5-3=2,
在Rt△A′FD中,由勾股定理可得A′D=A′F2+DF2=![]() =
=![]() ,
,
故选C.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目