题目内容
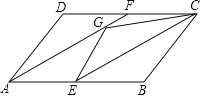
【题目】在ABCD中,点E为AB边的中点,连接CE,将△BCE沿着CE翻折,点B落在点G处,连接AG并延长,交CD于F.
(1)求证:四边形AECF是平行四边形;
(2)若CF=5,△GCE的周长为20,求四边形ABCF的周长.
【答案】(1)见解析;(2)30
【解析】
(1)由平行四边形的性质得出AE∥FC,再由三角形的外角的性质,以及折叠的性质,可以证明∠FAE=∠CEB,进而证明AF∥EC,即可得出结论;
(2)由折叠的性质得:GE=BE,GC=BC,由△GCE的周长得出GE+CE+GC=20,BE+CE+BC=20,由平行四边形的性质得出AF=CE,AE=CF=5,即可得出结果.
(1)证明:∵四边形ABCD是平行四边形,
∴AE∥FC,
∵点E是AB边的中点,
∴AE=BE,
∵将△BCE沿着CE翻折,点B落在点G处,
∴BE=GE,∠CEB=∠CEG,
∴AE=GE,
∴∠FAE=∠AGE,
∵∠CEB=∠CEG=![]() ∠BEG,∠BEG=∠FAE+∠AGE,
∠BEG,∠BEG=∠FAE+∠AGE,
∴∠FAE=![]() ∠BEG,
∠BEG,
∴∠FAE=∠CEB,
∴AF∥EC,
∴四边形AECF是平行四边形;
(2)解:由折叠的性质得:GE=BE,GC=BC,
∵△GCE的周长为20,
∴GE+CE+GC=20,
∴BE+CE+BC=20,
∵四边形AECF是平行四边形,
∴AF=CE,AE=CF=5,
∴四边形ABCF的周长=AB+BC+CF+AF=AE+BE+BC+CE+CF=5+20+5=30.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目