题目内容
 已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为
已知:如图所示,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=4cm2,则阴影部分的面积为分析:易得△ABD,△ACD为△ABC面积的一半,同理可得△BEC的面积等于△ABC面积的一半,那么阴影部分的面积等于△BEC的面积的一半.
解答:解:∵D为BC中点,根据同底等高的三角形面积相等,
∴S△ABD=S△ACD=
S△ABC=
×4=2,
同理S△BDE=S△CDE=
S△BCE=
×2=1,
∴S△BCE=2,
∵F为EC中点,
∴S△BEF=
S△BCE=
×2=1.
故答案为1.
∴S△ABD=S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
同理S△BDE=S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△BCE=2,
∵F为EC中点,
∴S△BEF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为1.
点评:此题考查了三角形中线的性质,解答此题的关键是知道同底等高的三角形面积相等.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
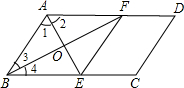 阅读下述说明过程,讨论完成下列问题:
阅读下述说明过程,讨论完成下列问题: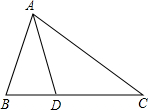 已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
已知:如图所示,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.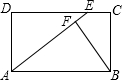 已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.
已知:如图所示,在矩形ABCD中,E为DC上的一点,BF⊥AE于点F,且BF=BC,求证:AE=AB.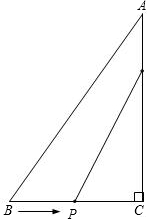 同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动.
同时出发,其中点P以1厘米/秒的速度沿着线段BC向点C运动,点Q以2厘米/秒的速度沿着线段CA向点A运动. 点M,连接DC.
点M,连接DC.