题目内容
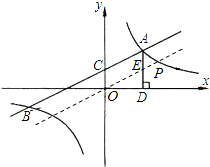
【题目】如图,一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= , k2=;
(2)根据函数图象可知,当y1>y2时,x的取值范围是;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.
【答案】
(1)![]() ;16
;16
(2)﹣8<x<0或x>4
(3)
解:由(1)知, ![]() .
.
∴m=4,点C的坐标是(0,2)点A的坐标是(4,4).
∴CO=2,AD=OD=4.
∴ ![]() .
.
∵S梯形ODAC:S△ODE=3:1,∴S△ODE= ![]() S梯形ODAC=
S梯形ODAC= ![]() ×12=4,
×12=4,
即 ![]() ODDE=4,
ODDE=4,
∴DE=2.
∴点E的坐标为(4,2).
又点E在直线OP上,
∴直线OP的解析式是 ![]() .
.
∴直线OP与 ![]() 的图象在第一象限内的交点P的坐标为(
的图象在第一象限内的交点P的坐标为( ![]() ).
).
故答案为: ![]() ,16,﹣8<x<0或x>4
,16,﹣8<x<0或x>4
【解析】解:(1)∵一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,m)和B(﹣8,﹣2),
的图象交于点A(4,m)和B(﹣8,﹣2),
∴K2=(﹣8)×(﹣2)=16,
﹣2=﹣8k1+2
∴k1= ![]()
2)∵一次函数y1=k1x+2与反比例函数 ![]() 的图象交于点A(4,4)和B(﹣8,﹣2),
的图象交于点A(4,4)和B(﹣8,﹣2),
∴当y1>y2时,x的取值范围是
﹣8<x<0或x>4;
【考点精析】认真审题,首先需要了解一次函数的图象和性质(一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远),还要掌握反比例函数的图象(反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点)的相关知识才是答题的关键.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案