题目内容
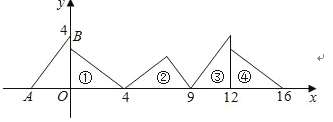
【题目】如图,数轴上有A,B两点,AB=18,原点O是线段AB上的一点,OA=2OB.
(1)求出A,B两点所表示的数;
(2)若点C是线段AO上一点,且满足 AC=CO+CB,求C点所表示的数;
(3)若点E以3个单位长度/秒的速度从点A沿数轴向点B方向匀速运动,同时点F以1个单位长度/秒的速度从点B沿数轴向右匀速运动,并设运动时间为t秒,问t为多少时,E、F两点重合.并求出此时数轴上所表示的数.
![]()
【答案】(1)A,B两点所表示的数分别是﹣12,6;(2)C点所表示的数是﹣2;(3)t=9时,E、F两点重合,数轴上所表示的数为15.
【解析】
(1)由OA=2OB,OA+OB=18即可求出OA、OB;
(2)设OC=x,则AC=12﹣x,BC=6+x,根据AC=CO+CB列出方程即可解决;
(3)由点E运动路程=18+点F运动路程,可列方程,可求t的值.
解:(1)∵OA+OB=AB=18,且OA=2OB
∴OB=6,OA=12,
∴A,B两点所表示的数分别是﹣12,6;
(2)设OC=x,则AC=12﹣x,BC=6+x,
∵AC=CO+CB,
∴12﹣x=x+6+x,
∴x=2,
∴OC=2,
∴C点所表示的数是﹣2;
(3)根据题意得:3t=18+t,
∴t=9
∴当t=9时,E、F两点重合,
此时数轴上所表示的数为OB+9=6+9=15.

【题目】科技馆门票价格规定如下表:
购票张数 |
|
| 100张以上 |
每张票的价格 | 18元 | 15元 | 10元 |
风鸣学校七年级![]() 、
、![]() 两个科技班共103人去科技馆,其中
两个科技班共103人去科技馆,其中![]() 班有40多人不足50人
班有40多人不足50人![]() 经计算,如果两个班都以班为单位购票,则一共应付1686元.
经计算,如果两个班都以班为单位购票,则一共应付1686元.
![]() 如果两个班联合起来,作为一个团体购票,可以省______元
如果两个班联合起来,作为一个团体购票,可以省______元![]()
![]() 七年级
七年级![]() 班有多少学生?
班有多少学生?
![]() 如果七年级
如果七年级![]() 班单独组织去科技馆,作为组织者,你如何购票才最省钱?
班单独组织去科技馆,作为组织者,你如何购票才最省钱?
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产![]() 、
、![]() 两种产品共50件.已知生产一件
两种产品共50件.已知生产一件![]() 种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件
种产品需用甲种原料9千克,乙种原料3千克,可获利润700元;生产一件![]() 种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
种产品需用甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产![]() 种产品
种产品![]() 件,完成表格:
件,完成表格:
|
| |
生产数量(件 |
| 件 |
需甲种原料(千克) |
|
|
需乙种原料(千克) |
|
|
(2)按要求安排![]() 、
、![]() 两种产品的件数有几种方案?请你设计出来.
两种产品的件数有几种方案?请你设计出来.
(3)以上方案哪种利润最大?是多少元?