题目内容
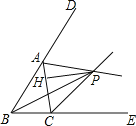
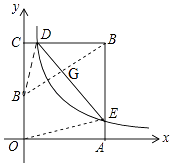
【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y= ![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE. 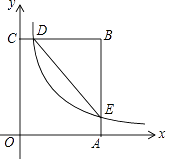
(1)连接OE,若△EOA的面积为3,则k=;
(2)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】
(1)6
(2)解:连接DB′,
设D( ![]() ,5),E(3,
,5),E(3, ![]() ),
),
∴BD=3﹣ ![]() ,BE=5﹣
,BE=5﹣ ![]() ,
,
∴tan∠BDE= ![]() =
= ![]() =
= ![]() ,
,
∵B与B′关于DE对称,
∴DE是BB′的中垂线,
∴BB′⊥DE,BG=B′G,DB′=BD,
∴∠DGB=90°,
∴∠BDE+∠DBB′=90°,
∠CB′B+∠DBB′=90°,
∴∠BDE=∠CB′B,
∴tan∠BDE=tan∠CB′B= ![]() =
= ![]() =
= ![]() ,
,
∴CB′= ![]() ,
,
设CD=x,则BD=B′D=3﹣x,
则 ![]() ,
,
∴x= ![]() ,
,
∴D( ![]() ,5).
,5).
【解析】解:(1)连接OE,如图1,
∵Rt△AOE的面积为3,
∴k=2×3=6.
所以答案是:6;
【考点精析】根据题目的已知条件,利用比例系数k的几何意义的相关知识可以得到问题的答案,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】为了支持国货,哈市某手机卖场计划用![]() 万元购进华为品牌手机.从卖场获知华为品牌
万元购进华为品牌手机.从卖场获知华为品牌![]() 种不同型号的手机的进价及售价如下表:
种不同型号的手机的进价及售价如下表:
|
|
| |
进价(元/部) |
|
|
|
售价(元/部) |
|
|
|
若该手机卖场同时购进两种不同型号的手机![]() 台,
台,![]() 万元刚好用完.
万元刚好用完.
(1)请您确定该手机的进货方案,并说明理由;
(2)该卖场老板准备把这批手机销售的利润![]() 的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?
的捐给公益组织,在同时购进两种不同型号的手机方案中,为了使捐款最多,你选择哪种方案?