题目内容
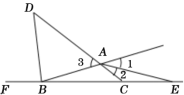
【题目】如图,在△ABC中,∠ABC<∠BCA<∠BAC,∠BAC和∠ABC的外角平分线AE、BD分别与BC、CA的延长线交于E、D.若AB=AE,BD=BA.则∠BCA的度数为____.
【答案】36°
【解析】
设∠ABC=x,由∠ABC=∠AEB,则∠AEB=x,根据三角形外角的性质得到∠1=∠ABC+∠AEB=2x,则∠2=2x,利用对顶角相等得∠3=∠D=4x,再根据三角形外角的性质得∠BCA=∠2+∠AEC=3x,∠FBD=∠D+∠BCD=7x,则∠DBA=∠FBD=7x,在△BCD中利用三角形的内角和定理可得到关于x的方程,解出x,然后求得∠BCA的度数.
设∠ABC=x,
∵∠ABC=∠AEB,
∴∠AEB=x,
∴∠1=∠ABC+∠AEB=2x,
∴∠2=2x,
∴∠3=∠D=4x,∠BCA=∠2+∠AEC=3x,
∴∠FBD=∠D+∠BCD=7x,
∴∠DBA=∠FBD=7x,
∴7x+7x+x=180°,解得x=12°,
∴∠BCA=3x=36°.
故填:36°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目