题目内容
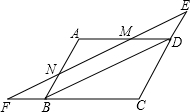四边形ABCD是平行四边形，直线EF∥BD，并且与CD、CB的延长线分别交于E、F，交AB、AD于N、M，求证：EN=FM．考点：平行四边形的性质
专题：证明题
分析：首先证明四边形BDMF和四边形BDEN是平行四边形，所以NE=BD，FM=BD，所以FN=EM，即EN=FM．
解答：证明：∵四边形ABCD是平行四边形，
∴AD‖BC，AB‖CD，
又∵EF‖BD，
∴四边形BDMF和四边形BDEN是平行四边形，
∴NE=BD，FM=BD，
∴FN=ME
∴FN+NM=ME+NM，
即EN=FM．
∴AD‖BC，AB‖CD，
又∵EF‖BD，
∴四边形BDMF和四边形BDEN是平行四边形，
∴NE=BD，FM=BD，
∴FN=ME
∴FN+NM=ME+NM，
即EN=FM．
点评：本题考查了平行四边形的判定和性质，解题的关键是熟记平行四边形的各种判定方法并且熟练运用．
练习册系列答案
相关题目
某中学生暑期环保小组的同学，随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量，数据如下：6，5，7，8，7，5，8，10，5，9（单位：个）．利用这些数据估计该小区2 000户家庭一周内需要环保方便袋约（ ）
| A、2 000个 |
| B、14 000个 |
| C、21 000个 |
| D、98 000个 |
下列运算正确的是（ ）
A、
| ||||||
B、3
| ||||||
C、2+
| ||||||
D、a
|
如果不等式组
的解集是x＞4，则n的范围是（ ）
|
| A、n≥4 | B、n≤4 |
| C、n=4 | D、n＜4 |
如图，AD是△ABC的中线，E、F分别是AB、AC的中点．