题目内容
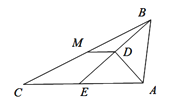
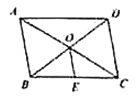
【题目】如图,![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,点
,点![]() 为
为![]() 中点,若
中点,若![]() 的周长为28,
的周长为28,![]() ,则
,则![]() 的周长为( )
的周长为( )
A.12B.17C.19D.24
【答案】A
【解析】
由四边形ABCD是平行四边形,根据平行四边形的性质可得OB=OD,再由E是CD中点,即可得BE=![]() BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=
BC,OE是△BCD的中位线,由三角形的中位线定理可得OE=![]() AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
AB, 再由ABCD的周长为28,BD=10, 即可求得AB+BC=14,BO=5,由此可得BE+OE=7, 再由△OBE的周长为=BE+OE+BO即可求得△OBE的周长.
∵四边形ABCD是平行四边形,
∴O是BD中点, OB=OD,
又∵E是CD中点,
∴BE=![]() BC,OE是△BCD的中位线,
BC,OE是△BCD的中位线,
∴OE=![]() AB,
AB,
∵ABCD的周长为28,BD=10,
∴AB+BC=14,
∴BE+OE=7,BO=5
∴△OBE的周长为=BE+OE+BO=7+5=12.
故选A.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目