题目内容
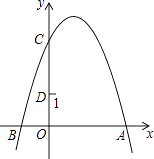
【题目】已知：如图一次函数y= 
x+1的图象与x轴交于点A，与y轴交于点B；二次函数y= x2+bx+c的图象与一次函数y= x+1的图象交于B、C两点，与x轴交于D、E两点且D点坐标为（1，0）．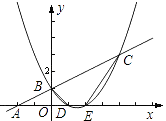
（1）求二次函数的解析式；
（2）求四边形BDEC的面积S；
（3）在x轴上是否存在点P，使得△PBC是以P为直角顶点的直角三角形？若存在，求出所有的点P，若不存在，请说明理由．
【答案】
（1）
解：将B（0，1），D（1，0）的坐标代入y= 
x2+bx+c，
得：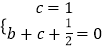 
，
得解析式y= x2﹣ 
x+1
（2）
解：设C（x0，y0）（x0≠0，y0≠0），
则有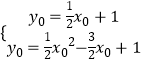 
解得 
，
∴C（4，3）
由图可知：S四边形BDEC=S△ACE﹣S△ABD，又由对称轴为x= 可知E（2，0），
∴S= AEy0﹣ AD×OB= ×4×3﹣ ×3×1= 
（3）
解：设符合条件的点P存在，令P（a，0）：
当P为直角顶点时，如图：过C作CF⊥x轴于F；
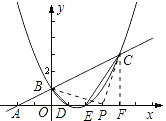
∵∠BPO+∠OBP=90°，∠BPO+∠CPF=90°，
∴∠OBP=∠FPC，
∴Rt△BOP∽Rt△PFC，
∴ 
，
即 
，
整理得a2﹣4a+3=0，
解得a=1或a=3；
∴所求的点P的坐标为（1，0）或（3，0），
综上所述：满足条件的点P共有2个．
【解析】（1）根据直线BC的解析式，可求得点B的坐标，由于B、D都在抛物线的图象上，那么它们都满足该抛物线的解析式，通过联立方程组即可求得待定系数的值．（2）根据抛物线的解析式，可求得E点的坐标，联立直线BC的解析式，可求得C点坐标；那么四边形BDEC的面积即可由△AEC、△ABD的面积差求得．（3）假设存在符合条件的P点，连接BP、CP，过C作CF⊥x轴于F，若∠BPC=90°，则△BPO∽△CPF，可设出点P的坐标，分别表示出OP、PF的长，根据相似三角形所得比例线段即可求得点P的坐标．
【考点精析】利用二次函数的性质对题目进行判断即可得到答案，需要熟知增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
