题目内容
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是BD弧上的一点,OE⊥BD于点G,连接AE交BC于点F,AC是⊙O的切线. 
(1)求证:∠ACB=2∠EAB;
(2)若cos∠ACB= ![]() ,AC=10,求BF的长.
,AC=10,求BF的长.
【答案】
(1)证明:连接AD,
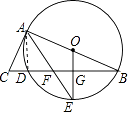
∵AB是⊙O的直径,
∴∠ADB=90°,
∵AC是⊙O的切线,
∴∠CAB=90°,
∴∠C+∠CAD=∠CAD+∠DAB=90°,
∴∠C=∠DAB,
∵OE⊥BD,
∴2 ![]() =
= ![]() ,
,
∴∠BAE= ![]() BDA,
BDA,
∴∠ACB=2∠EAB
(2)解:∵cos∠ACB= ![]() ,AC=10,
,AC=10,
∴BC=25,
∴AB= ![]() =5
=5 ![]() ,
,
∵∠C=∠BAD,∠B=∠B,
∴△ABC∽△DBA,
∴ ![]() ,
,
∴BD= ![]() =21,
=21,
∵OE⊥BD,
∴BG=DG= ![]() ,
,
∵AD= ![]() =2
=2 ![]() ,
,
∵AO=BO,BG=DG,
∴OG= ![]() AD=
AD= ![]() ,
,
∴GE= ![]() ,
,
∵AD∥GE,
∴ ![]() =
= ![]() ,
,
∴FG= ![]() DG=
DG= ![]() ,
,
∴BF=BG+FG= ![]() +
+ ![]() =15.
=15.
【解析】(1)连接AD,由AB是⊙O的直径,得到∠ADB=90°,由AC是⊙O的切线,得到∠CAB=90°,根据余角的性质得到∠C=∠DAB,根据圆周角定理即可得到结论;(2)根据三角函数的定义得到BC=25,根据勾股定理得到AB= ![]() =5
=5 ![]() ,根据相似三角形的性质得到BD=
,根据相似三角形的性质得到BD= ![]() =21,根据垂径定理得到BG=DG=
=21,根据垂径定理得到BG=DG= ![]() ,根据平行线分线段成比例定理得到
,根据平行线分线段成比例定理得到 ![]() =
= ![]() ,于是得到结论.
,于是得到结论.
【考点精析】本题主要考查了垂径定理和切线的性质定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案