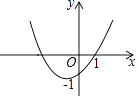题目内容
【题目】如图,在平面直角坐标系中,四边形ABCO为正方形,A点坐标为(0,2),点P为x轴负半轴上一动点,以AP为直角作等腰直角三角形APD,∠APD=90°(点D落在第四象限)
(1)当点P的坐标为(﹣1,0)时,求点D的坐标;
(2)点P在移动的过程中,点D是否在直线y=x﹣2上?请说明理由;
(3)连接OB交AD于点G,求证:AG=DG.
【答案】
(1)
解:如图1中,作DH⊥OC于H.

∵四边形AOCB是正方形,A(0,2),P(﹣1,0),
∴∠AOP=∠PHD=∠APD=90°,OA=2,OP=1,
∵∠APO+∠DPH+90°,∠DPH+∠PDH=90°,
∴∠APO=∠PDH,
在△APO和△PDH中,
 ,
,
∴△APO≌△PDH,
∴PH=OA=2,DH=OP=1,
∴OH=1,
∴D(1,﹣1)
(2)
解:如图2中,作射线CD,设AD交PC于G.

∵∠GCA=∠GDP=45°,∠AGC=∠PGD,
∴△AGC∽△PGD,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,∵∠AGP=∠CGD,
,∵∠AGP=∠CGD,
∴△AGP∽△CGD,
∴∠PAG=∠GCD=45°,
∴∠ACD=90°,
∴CD⊥AC,
∵直线AC的解析式为y=﹣x+2,
∴直线CD的解析式为y=x﹣2,
∴点D在直线CD上
(3)
解:如图3中,连接CG、AC、CD.

∵四边形OABC是正方形,
∴BA=BC,∠GBA=∠GBC,∵BG=BG,
∴△GBA≌△GBC,
∴GA=GC,
∴∠GAC=∠GCA,
∵∠ACD=90°,
∴∠GDC+∠GAC=90°,∠GCB+∠GCA=90°,
∴∠GDC=∠GCD,
∴GC=GD,
∴AG=GD
【解析】(1)如图1中,作DH⊥OC于H.只要证明△APO≌△PDH,推出PH=OA=2,DH=OP=1即可.(2)如图2中,作射线CD,设AD交PC于G.由△AGC∽△PGD,推出 ![]() =
= ![]() ,推出
,推出 ![]() =
= ![]() ,由∠AGP=∠CGD,推出△AGP∽△CGD,推出∠PAG=∠GCD=45°,推出∠ACD=90°,即CD⊥AC,求出直线CD的解析式即可解决问题.(3)如图3中,连接CG、AC、CD.由△GBA≌△GBC,推出GA=GC,只要证明GC=GD即可解决问题.
,由∠AGP=∠CGD,推出△AGP∽△CGD,推出∠PAG=∠GCD=45°,推出∠ACD=90°,即CD⊥AC,求出直线CD的解析式即可解决问题.(3)如图3中,连接CG、AC、CD.由△GBA≌△GBC,推出GA=GC,只要证明GC=GD即可解决问题.
【考点精析】本题主要考查了相似三角形的应用的相关知识点,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解才能正确解答此题.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分; 表1:栽下的各品种树苗棵数统计表表
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 |
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共棵,乙品种树苗棵.
(2)图1中,甲%、乙%;
(3)已知这批树苗成活率为90%,将图2补充完整.