题目内容
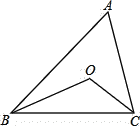
【题目】如图,在![]() ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
ABC中,BO、CO分别平分∠ABC和∠ACB.计算:
(1)若∠A ![]() 60°,求∠BOC的度数;
60°,求∠BOC的度数;
(2)若∠A ![]() 100°, 则∠BOC的度数是多少?
100°, 则∠BOC的度数是多少?
(3)若∠A ![]() 120°, 则∠BOC的度数又是多少?
120°, 则∠BOC的度数又是多少?
(4)由(1)、(2)、(3),你发现了什么规律?请用一个等式将这个规律表示出来.
【答案】(1)∠BOC![]() 120°;(2)∠BOC
120°;(2)∠BOC![]() 140°;(3)∠BOC=150°;(4)∠BOC=90°+
140°;(3)∠BOC=150°;(4)∠BOC=90°+![]() ∠A
∠A
【解析】
(1)根据BO、CO分别平分∠ABC和∠ACB可得: ∠CBO+∠BCO的值,再根据三角形内角和得出∠BOC;
(2)、(3)同理(1)可求得;
(4)根据(1)-(3)规律可得.
(1)∵BO、CO分别平分∠ABC和∠ACB.∠A ![]() 600
600
∴∠CBO+∠BCO![]()
![]() (1800
(1800![]() ∠A)
∠A)![]()
![]() (1800
(1800![]() 600)
600)![]() 600
600
∴∠BOC![]() 1800
1800![]() (∠CBO+∠BCO)
(∠CBO+∠BCO)![]() 1800
1800![]() 600
600![]() 1200
1200
(2)同理,若∠A ![]() 1000, 则∠BOC
1000, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 140
140
(3)同理,若∠A ![]() 1200, 则∠BOC
1200, 则∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A![]() 1500
1500
(4)由(1)、(2)、(3),发现:∠BOC![]() 1800
1800![]()
![]() (1800
(1800![]() ∠A)
∠A)![]() 900+
900+![]() ∠A
∠A

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目