题目内容
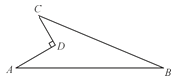
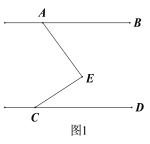
【题目】如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿射线CD平移至FG.
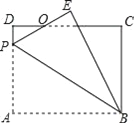
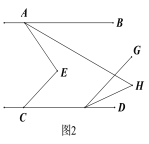
①如图2,若∠AEC=90°,FH平分∠DFG,求∠AHF的度数;
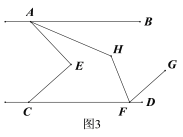
②如图3,若FH平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
【答案】(1)见解析;(2)①45°;②∠AHF=90°+![]() ∠AEC(或2∠AHF-∠AEC=180°),理由见解析.
∠AEC(或2∠AHF-∠AEC=180°),理由见解析.
【解析】
(1)过E作EF∥AB,可得∠A=∠AEN,利用平行于同一条直线的两直线平行得到EN与CD平行,再得到一对内错角相等,进而得出答案;
(2)①HF平分∠DFG,设∠GFH=∠DFH=x,根据平行线的性质可以得到∠AHF的度数,再由∠AEC=90°,根据角的关系易得∠AHF的度数;②设∠GFD=2x,∠BAH=∠EAH=y,根据角平分线的性质以及(1)中结论即可得到∠AHF与∠AEC的数量关系.
(1)如图1,过点E作直线EN∥AB,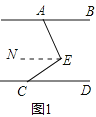
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAE+∠ECD;
(2)∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°-x,
如图2,过点H作l∥AB,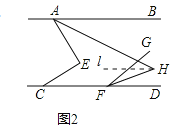
易证∠AHF=∠BAH+∠DFH=45°-x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°-x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,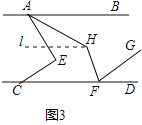
易证∠AHF-y+∠CFH=180°,
即∠AHF-y+90°-x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+![]() ∠AEC.(或2∠AHF-∠AEC=180°.)
∠AEC.(或2∠AHF-∠AEC=180°.)

【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布条形图.
最喜爱的传统文化项目类型频数分布表
项目类型 | 频数 | 频率 |
书法类 | 18 | a |
围棋类 | 14 | 0.28 |
喜剧类 | 8 | 0.16 |
国画类 | b | 0.20 |
根据以上信息完成下列问题: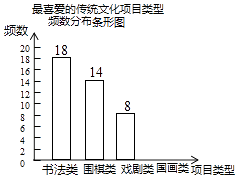
(1)直接写出频数分布表中a的值;
(2)补全频数分布条形图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?