题目内容
【题目】如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.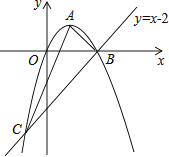
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x﹣1)2+1,
又抛物线过原点,
∴0=a(0﹣1)2+1,解得a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+1,
即y=﹣x2+2x,
联立抛物线和直线解析式可得 ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
∴B(2,0),C(﹣1,﹣3)
(2)
证明:如图,分别过A、C两点作x轴的垂线,交x轴于点D、E两点,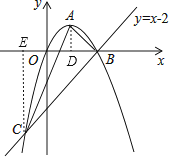
则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3,
∴∠ABO=∠CBO=45°,即∠ABC=90°,
∴△ABC是直角三角形;
(3)
解:假设存在满足条件的点N,设N(x,0),则M(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|,
由(2)在Rt△ABD和Rt△CEB中,可分别求得AB= ![]() ,BC=3
,BC=3 ![]() ,
,
∵MN⊥x轴于点N
∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时有 ![]() =
= ![]() 或
或 ![]() =
= ![]() ,
,
①当 ![]() =
= ![]() 时,则有
时,则有 ![]() ,即|x||﹣x+2|=
,即|x||﹣x+2|= ![]() |x|,
|x|,
∵当x=0时M、O、N不能构成三角形,
∴x≠0,
∴|﹣x+2|= ![]() ,即﹣x+2=±
,即﹣x+2=± ![]() ,解得x=
,解得x= ![]() 或x=
或x= ![]() ,
,
此时N点坐标为( ![]() ,0)或(
,0)或( ![]() ,0);
,0);
②当 ![]() =
= ![]() 时,则有
时,则有 ![]() ,即|x||﹣x+2|=3|x|,
,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1,
此时N点坐标为(﹣1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为( ![]() ,0)或(
,0)或( ![]() ,0)或(﹣1,0)或(5,0)
,0)或(﹣1,0)或(5,0)
【解析】(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)分别过A、C两点作x轴的垂线,交x轴于点D、E两点,结合A、B、C三点的坐标可求得∠ABO=∠CBO=45°,可证得结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得 ![]() =
= ![]() 或
或 ![]() =
= ![]() ,可求得N点的坐标. 本题为二次函数的综合应用,涉及知识点有待定系数法、图象的交点问题、直角三角形的判定、勾股定理、相似三角形的性质及分类讨论等.在(1)中注意顶点式的运用,在(3)中设出N、M的坐标,利用相似三角形的性质得到关于坐标的方程是解题的关键,注意相似三角形点的对应.本题考查知识点较多,综合性较强,难度适中.
,可求得N点的坐标. 本题为二次函数的综合应用,涉及知识点有待定系数法、图象的交点问题、直角三角形的判定、勾股定理、相似三角形的性质及分类讨论等.在(1)中注意顶点式的运用,在(3)中设出N、M的坐标,利用相似三角形的性质得到关于坐标的方程是解题的关键,注意相似三角形点的对应.本题考查知识点较多,综合性较强,难度适中.
【考点精析】本题主要考查了抛物线与坐标轴的交点和勾股定理的概念的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

【题目】如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.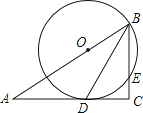
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
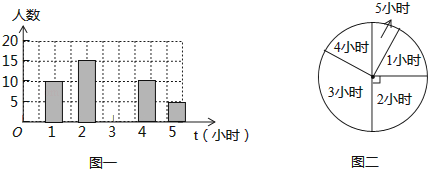
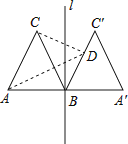
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
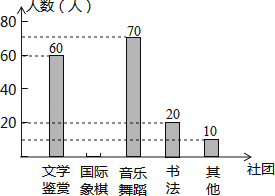
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.