题目内容
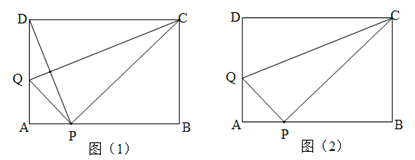
【题目】如图(1)将长方形纸片ABCD的一边CD沿着CQ向下折叠,使点D落在边AB上的点P处.
(1)试判断线段CQ与PD的关系,并说明理由;
(2)如图(2),若AB=CD=5,AD=BC=3.求AQ的长;
(3)如图(2),BC=3,取CQ的中点M,连接MD,PM,若MD⊥PM,求AQ(AB+BC)的值.
【答案】(1)见解析(2)![]() (3)9
(3)9
【解析】
(1)由折叠知CD=CP,∠DCQ=∠PCQ.根据等腰三角形三线合一的性质即可得出结论;
(2)设AQ=x,则DQ=QP=3-x.在Rt△PBC中,由勾股定理可得PB的长,进而得到AP的长.在Rt△APQ中,由勾股定理列方程,求解即可得出结论.
(3)由直角三角形斜边上的中线等于斜边的一半,得到DM=QM=MC=PM,由等腰三角形的性质得到∠MDQ=∠MQD,∠MQP=∠MPQ.再由四边形内角和为360°得到∠DQP=135°,从而得到∠AQP=45°,得到△APQ为等腰直角三角形,从而求出AQ的长.在Rt△PBC中,由勾股定理得到(AB-AQ)2+32=AB2,变形即可得到结论.
(1)CQ垂直平分DP.理由如下:
由折叠的性质可知:CD=CP,∠DCQ=∠PCQ,∴CQ垂直平分DP.
(2)设AQ=x,则DQ=QP=3-x.
∵PC=DC=5,BC=3,∴PB=![]() =4.
=4.
∵AB=5,∴AP=5-4=1.在Rt△APQ中,∵![]() ,∴
,∴![]() ,解得:x=
,解得:x=![]() ,∴AQ=
,∴AQ=![]() .
.
(3)如图,∵∠QDC=∠QPC=90°,M为斜边QC的中点,∴DM=QM=MC=PM,∴∠MDQ=∠MQD,∠MQP=∠MPQ.
∵MD⊥PM,∴∠DMP=90°,∴∠DQP=∠DQM+∠PQM=(360°-90°)÷2=135°,∴∠AQP=180°-135°=45°.
∵∠A=90°,∴∠APQ=∠AQP=45°,∴△APQ时等腰直角三角形,∴AP=AQ,DQ=PQ=![]() AQ.
AQ.
∵AQ+QD=AD=BC=3,∴(![]() +1)AQ=3,解得:AQ=3(
+1)AQ=3,解得:AQ=3(![]() -1)=
-1)=![]() .在Rt△PBC中,∵PB2+BC2=PC2,∴(AB-AQ)2+32=AB2,∴ABAQ=
.在Rt△PBC中,∵PB2+BC2=PC2,∴(AB-AQ)2+32=AB2,∴ABAQ=![]() (AQ2+9),∴AQ(AB+BC)= AQAB+ AQ BC=
(AQ2+9),∴AQ(AB+BC)= AQAB+ AQ BC=![]() (AQ2+9)+3AQ=
(AQ2+9)+3AQ=![]() (AQ+3)2=
(AQ+3)2=![]() =9.
=9.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案