题目内容
【题目】一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 叠合在一起,边
叠合在一起,边![]() 与
与![]() 重合,
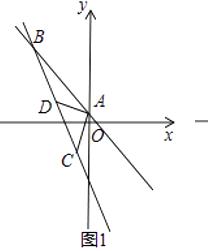
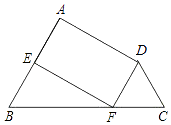
重合,![]() (如图1),点
(如图1),点![]() 为边
为边![]()
![]() 的中点,边
的中点,边![]() 与
与![]() 相交于点
相交于点![]() ,此时线段
,此时线段![]() 的长是 .现将三角板
的长是 .现将三角板![]() 绕点
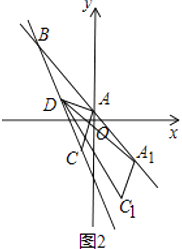
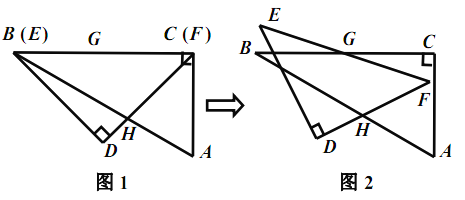
绕点![]() 按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在![]() 从
从![]() 到
到![]() 的变化过程中,点
的变化过程中,点![]() 相应移动的路径长共为 .(结果保留根号)
相应移动的路径长共为 .(结果保留根号)
【答案】12![]() -12.12
-12.12![]() -18.
-18.
【解析】
试题解析:如图1中,作HM⊥BC于M,HN⊥AC于N,则四边形HMCN是正方形,设边长为a.
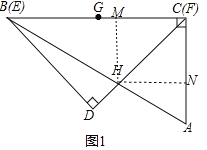
在Rt△ABC中,∵∠ABC=30°,BC=12,
∴AB=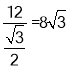 ,
,
在Rt△BHM中,BH=2HM=2a,
在Rt△AHN中,AH=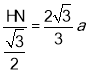 ,
,
∴2a+![]() ,
,
∴a=6![]() -6,
-6,
∴BH=2a=12![]() -12.
-12.
如图2中,当DG∥AB时,易证GH1⊥DF,此时BH1的值最小,易知BH1=BK+KH1=3![]() +3,
+3,
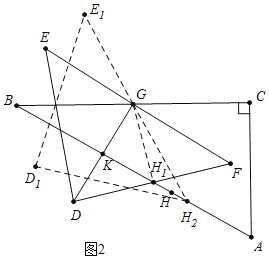
∴HH1=BH-BH1=9![]() -15,
-15,
当旋转角为60°时,F与H2重合,易知BH2=6![]() ,
,
观察图象可知,在∠CGF从0°到60°的变化过程中,点H相应移动的路径长=2HH1+HH2=18![]() -30+[6
-30+[6![]() -(12
-(12![]() -12)]=12
-12)]=12![]() -18.
-18.

练习册系列答案
相关题目
【题目】在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
则m与v之间的关系最接近于下列各关系式中的( )
A. v=2m-1B. v=m2-1C. v=3m-3D. v=m+1