题目内容
【题目】如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.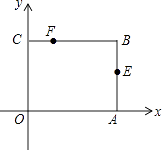
(1)点E的坐标为 , 点F的坐标为;
(2)点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
①点E′的坐标为 , 点F′的坐标为;
②求直线E′F′的解析式;
(3)若M为x轴上的动点,N为y轴上的动点,当四边形MNFE的周长最小时,求出点M,N的坐标,并求出周长的最小值.
【答案】
(1)(3,1),(1,2)
(2)(3,﹣1),F'(﹣1,2)
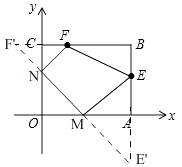
(3)解:如图,∵E(3,1),F(1,2),
∴EF= ![]() ,
,
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴连接E'F'和x轴交于M,和y轴交于N,此时四边形MNFE的周长最小,
∴NF=NF',ME=ME',
∵E'(3,﹣1),F'(﹣1,2),
∴E'F'= ![]() =5,
=5,
∴四边形MNFE的周长的最小值为NF+MN+ME+EF
=NF'+MN+ME'+EF=E'F'+EF=5+ ![]() .
.
【解析】解:(1)∵A(3,0),C(0,2),
∴OA=3,OC=2,
∵四边形OABC是矩形,
∴BC∥OA,OC∥AB,BC=OA=3,AB=OC=2,
∴B(3,2),
∵点E是AB的中点,
∴AE= ![]() AB=1,
AB=1,
∴E(3,1),
∵点F在BC上,且CF=1,
∴F(1,2),
所以答案是:(3,1),(1,2),
⑵①由(1)知,E(3,1),F(1,2),
∵点E关于x轴的对称点为E′,点F关于y轴的对称点为F′,
∴E'(3,﹣1),F'(﹣1,2),
所以答案是:(3,﹣1),F'(﹣1,2);
②设直线E'F'的解析式为y=kx+b,
∴ ![]() ,
,
∴ 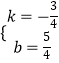 ,
,
∴直线E'F'的解析式为y=﹣ ![]() x+
x+ ![]() ;
;

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目