题目内容
【题目】如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F ， 且AF＝BD ， 连接BF ．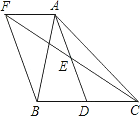 
（1）求证：BD＝CD；
（2）如果AB＝AC ， 试判断四边形AFBD的形状，并证明你的结论．
【答案】
（1）
解答：证明：∵AF∥BC，∴∠AFE＝∠DCE，∵E是AD的中点，∴AE＝DE， 
，∴△AEF≌△DEC（AAS），∴AF＝DC，∵AF＝BD，∴BD＝CD．
（2）
解答：四边形AFBD是矩形
理由：∵AB＝AC，D是BC的中点
∴AD⊥BC
∴∠ADB＝90°，
∵AF＝BD，
又∵过A点作BC的平行线交CE的延长线于点F，即AF∥BC
∴四边形AFBD是平行四边形，∴四边形AFBD是矩形．
【解析】（1）先由AF∥BC ， 利用平行线的性质可证∠AFE＝∠DCE ， 而E是AD中点，那么AE＝DE ， ∠AEF＝∠DEC ， 利用AAS可证△AEF≌△DEC ， 那么有AF＝DC ， 又AF＝BD ， 从而有BD＝CD；（2）四边形AFBD是矩形．由于AF平行等于BD ， 易得四边形AFBD是平行四边形，又AB＝AC ， BD＝CD ， 利用等腰三角形三线合一定理，可知AD⊥BC ， 即∠ADB＝90°，那么可证四边形AFBD是矩形．
【考点精析】利用等腰三角形的性质和矩形的判定方法对题目进行判断即可得到答案，需要熟知等腰三角形的两个底角相等（简称：等边对等角）；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．
练习册系列答案
相关题目
