��Ŀ����
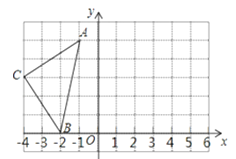
����Ŀ��������12�֣���ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���![]() ��mΪ��������ͼ����x�ύ�ڵ�A(��3��0)����y�ύ�ڵ�C����ֱ��x��1Ϊ�Գ����������y��ax2��bx��c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B
��mΪ��������ͼ����x�ύ�ڵ�A(��3��0)����y�ύ�ڵ�C����ֱ��x��1Ϊ�Գ����������y��ax2��bx��c��a��b��cΪ��������a��0������A��C���㣬����x��������ύ�ڵ�B
(1) ��m��ֵ�������ߵĺ�������ʽ;
(2) �Ƿ������������һ����Q��ʹ����ACQ����ACΪֱ�DZߵ�ֱ�������Σ������ڣ������Q�ĺ����ꣻ�����ڣ���˵������;
(3) ��P�������߶Գ�����һ���㣬��ʹ��ACP�ܳ���С������P������һ����y�ƽ�е�ֱ�߽���������M1(x1��y1)��M2(x2��y2)���㣬����![]() �Ƿ�Ϊ��ֵ������ǣ��������������������˵������. ���ο���ʽ����ƽ��ֱ������֮�У���A((x1��y1)��B(x2��y2)����A��B�����ľ���Ϊ
�Ƿ�Ϊ��ֵ������ǣ��������������������˵������. ���ο���ʽ����ƽ��ֱ������֮�У���A((x1��y1)��B(x2��y2)����A��B�����ľ���Ϊ![]() ��
��

���𰸡�����(1) ![]() ��
��![]()
(2) ����. ��Q(x��![]() )
)
�� ����CΪֱ�Ƕ���ʱ,����ACO����CQE,��x��5.2;
����AΪֱ�Ƕ���ʱ,����ACO����AQE,��x��8.2;
����������Q��ĺ�����Ϊ5.2��8.2.
(3) ֱ��BC�Ľ���ʽΪ![]() ,��P(1��3)
,��P(1��3)
�����P��ֱ��Ϊ��y��kx��3��k,
����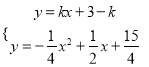 ��������x2��(4k��2)x��4k��3��0.
��������x2��(4k��2)x��4k��3��0.
��x1��x2��2��4k��x1x2����4k��3��y1��y2��k(x1��x2)
��![]()
ͬ����![]() ��
��![]()
��![]() , (��ע�����)
, (��ע�����)
��![]() Ϊ��ֵ.
Ϊ��ֵ.
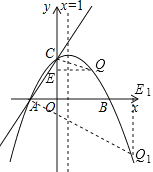
�������������������1���������m��ֵ�����������߶Գ��Եõ�B�����꣬����A��B���������ý���ʽ��������ߵĽ���ʽ��
��2����4���ʽ�Ϊ���ӣ����ͼ��ʾ���ּ�����������
��1����ȷ����ʱ��ACP���ܳ���С��������ԳƵ����ʺ�����֮���߶���̵�ԭ�������
��2����ȷ��P������P��1��3�����Ӷ�ֱ��M1M2�Ľ���ʽ���Ա�ʾΪy=kx+3-k��
��3�������ø���ϵ����ϵ���M1��M2���������Ĺ�ϵ���õ�x1+x2=2-4k��x1x2=-4k-3����һ����Ϊ�˺����ĸ��Ӽ���������
��4�������������ľ��빫ʽ���ֱ�����߶�M1M2��M1P��M2P�ij��ȣ���Ƚϼ��ɵõ����ۣ� ![]() Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�
Ϊ��ֵ����һ���漰���������㣬ע�ⲻҪ�������������Եó����Ľ��ۣ�
��3���֢���CΪֱ�Ƕ��㣬��ACO�����ڡ�CQE������AΪֱ�Ƕ��㣬��ACO������
��AQE���������������⣮
���������
����(1) ![]() ��
��![]()
(2) ����. ��Q(x��![]() )
)
�� ����CΪֱ�Ƕ���ʱ,����ACO����CQE,��x��5.2;
����AΪֱ�Ƕ���ʱ,����ACO����AQE,��x��8.2;
����������Q��ĺ�����Ϊ5.2��8.2.
() ֱ��BC�Ľ���ʽΪ![]() ,��P(1��3)
,��P(1��3)
�����P��ֱ��Ϊ��y��kx��3��k,
���� ��������x2��(4k��2)x��4k��3��0.
��������x2��(4k��2)x��4k��3��0.
��x1��x2��2��4k��x1x2����4k��3��y1��y2��k(x1��x2)
��![]()
ͬ����![]() ��
��![]()
��![]() , (��ע�����)
, (��ע�����)
��![]() Ϊ��ֵ.
Ϊ��ֵ.

 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�