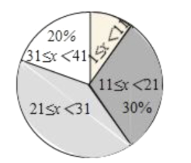
题目内容
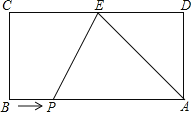
【题目】矩形
与矩形
如图放置，点
共线，点
共线，连接
，取的中点
，连接
.若
，则的长为
A. 
B. 
C. 
D. 
【答案】A
【解析】
延长GH交AD于点P，先证△APH≌△FGH得AP=GF=1，GH=PH=
PG，再利用勾股定理求得PG=2
，从而得出答案．
解：如图，延长GH交AD于点P，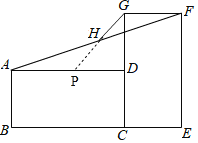
∵四边形ABCD和四边形CEFG都是矩形，
∴∠ADC=∠ADG=∠CGF=90°，AD=BC=3、GF=CE=1，
∴AD∥GF，
∴∠GFH=∠PAH，
又∵H是AF的中点，
∴AH=FH，
在△APH和△FGH中，
∵
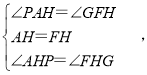
∴△APH≌△FGH（ASA），
∴AP=GF=1，GH=PH=PG，
∴PD=AD-AP=3-1=2，
∵CG=EF=3、CD=1，
∴DG=2，△DGP是等腰直角三角形，
则GH=PG= ×
故选：A．
练习册系列答案
相关题目
【题目】学校为了从李飞与刘亮中选取一人参加市射击比赛，现将他们某次射击训练的成绩绘制了如下图所示的折线统计图：
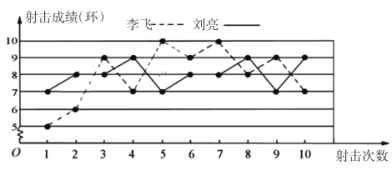
（1）请根据折线统计图中提供的信息填写下表：
平均数 | 中位 | 众数 | |
李飞 | 8 | ||
刘亮 | 8 | 8 |
（2）请计算李飞与刘亮射击训练的成绩的方差．（方差公式：
）
（3）从折线统计图上分析李飞与刘亮的射击成绩走势和稳定性，派谁去参加射击比赛更合适．
