题目内容
如图,在矩形ABCD中,AB=4,AD=10,直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),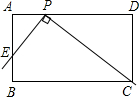 一直角边经过点C,另一直角边AB交于点E,我们知道,结论“Rt△AEP∽Rt△DPC”成立.
一直角边经过点C,另一直角边AB交于点E,我们知道,结论“Rt△AEP∽Rt△DPC”成立.(1)当∠CPD=30°时,求AE的长;
(2)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.
分析:(1)由于∠CPD与∠AEP同为∠APE的余角,因此当∠DPC=30°时,∠AEP=30°.可在Rt△CPD中,根据∠CPD的度数和CD的长,求出PD的长,进而可求出AP的值.同理可在Rt△APE中,求出AE的长.
(2)由于Rt△AEP∽Rt△DPC,当△DPC的周长等于△AEP周长的2倍时,两个三角形的相似比为1:2,即
=
=
=2,根据CD=AB=4,可求出PD的长.
(2)由于Rt△AEP∽Rt△DPC,当△DPC的周长等于△AEP周长的2倍时,两个三角形的相似比为1:2,即
| CD |
| AP |
| PD |
| AE |
| PC |
| PE |
解答:解:(1)∵∠CPD=90°-∠APE=∠AEP,
∴当∠CPD=30°时,∠AEP=30°.
在Rt△CPD中,CD=AB=4,∠CPD=30°,因此PD=CD•cot30°=4
,
∴AP=AD-PD=10-4
.
在Rt△APE中,AP=10-4
,∠AEP=30°,因此AE=AP•cot30°=10
-12.
(2)假设存在这样的点P,
∵Rt△AEP∽Rt△DPC,
∴
=
=2.
∵CD=AB=4,
∴AP=2,PD=8,
∴存在这样的P点,且DP长为8.
∴当∠CPD=30°时,∠AEP=30°.
在Rt△CPD中,CD=AB=4,∠CPD=30°,因此PD=CD•cot30°=4
| 3 |
∴AP=AD-PD=10-4
| 3 |
在Rt△APE中,AP=10-4
| 3 |
| 3 |
(2)假设存在这样的点P,
∵Rt△AEP∽Rt△DPC,
∴
| CD |
| AP |
| PD |
| AE |
∵CD=AB=4,
∴AP=2,PD=8,
∴存在这样的P点,且DP长为8.
点评:本题考查的是相似三角形和直角三角形的性质,属中学阶段的常规题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点A出发以1cm/s的速度向点B运动,点Q从点B出发以2cm/s的速度向点C运动,设经过的时间为xs,△PBQ的面积为ycm2,则下列图象能反映y与x之间的函数关系的是( )



 .
. 动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象.
动过程中,Q点停留了1s,图②是P、Q两点在折线AB-BC-CD上相距的路程S(cm)与时间t(s)之间的函数关系图象. 如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( ) DE,EF与AB交于点F,设CE=x,BF=y.
DE,EF与AB交于点F,设CE=x,BF=y.